ここで、ω(オメガ)は角振動数と呼ばれ、普通の振動数の2π倍で下式のように周期 T と逆数の関係にある。
スピーカーの性能を評価するとき、群遅延特性あるいは群遅延時間という項目を目にすることがある。一言でいうと、例えば手を叩くときに発するような瞬間的な音(トーンバースト)がスピーカーから出るとき、少し遅れて出力されるという現象である。しかし、何故このような現象が起こるのかを理解するのは結構難しい。少し詳しいテキストをひもとくと、群遅延時間(td ) とは、位相シフトの周波数微分値であると書いてある。しかし、これでは何のことだか分からない。
これを、説明するには、やはり波の性質を数学的に表す場合どうしても必要なフーリエ解析(分解、合成)の原理を知っておく必要があるので始めに簡単に説明しておく。すでにご存知の方はトーンバースト信号の項へスキップして下さい。スピーカーの群遅延特性のみに興味ある方はこちらへ。
いうまでもなく、音は空気圧の変化が波として伝わる現象で、ある地点での音は、その場所の圧力差の時間変化ΔP(t )で表せる。これを、マイクで電気に変換すれば電圧の時間変化V(t )として表せる。これらを波形とよびf (t )と書くことにする。フランスの数学者フーリエは時間 t1からt2の間の如何なる波形 f (t ) も T=t2-t1 を周期とするサイン・コサイン波およびその高調波の和で表せることを示した。式で書けば、
![]()
ここで、ω(オメガ)は角振動数と呼ばれ、普通の振動数の2π倍で下式のように周期 T と逆数の関係にある。
![]()
an,bn はフーリエ係数と呼ばれ
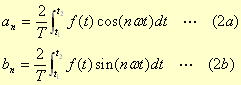
と、もとの波形から求まる。(1)式をフーリエ級数、(2)式をフーリエ積分とよぶ。
また、時間の関数である f(t) を 角振動数 nωの関数であるフーリエ係数に変換することをフーリエ変換という。(通常は、t1=−∽、t2=∽ の場合についてこう呼ぶ)
ここで、注意する必要があるのは、周期 T の選び方である。 例えばある楽器の音色を表す場合、T はその時の基音 f0 に対応する周期 T=1/f (100 Hz なら 0.01秒)を取るのではなく、その楽器の音色を表現するに十分な時間(例えば1秒間)にしておくことである。これを、(サンプリング)時間窓と呼ぶことにする。
この場合、フーリエ級数(1)式は、この時間窓内の音を正確に表すが、その外側(t < t1、t>t2)では、窓内の波形を周期 Tで繰り返す波形となり、もとの波形を全て(全時間帯にわたって)表すわけではない。
最近、FFT(高速フーリエ変換器) という測定器が音質評価などにも使われるが、これは時々刻々変化する音に対し適当なサンプリング時間窓(時間巾設定可能)に対するフーリエ変換((2)式の積分の実行)をリアルタイムで行い周波数スペクトル(an、bn )を求めCRT上に表示する装置のことである。
ここで、既に少し波の勉強をした人は意外に思われるかも知れないが、(1)式には位相φを使っていない。一方、よく音は周波数強度と位相差(又は時間差)によって表せると書いてある場合が多いが、位相を入れて表すことも可能である。すなわち、(1)式は
![]()
と表すことも可能で(サイン又はコサイン関数のみで展開する場合)この場合は各周波数成分についての位相φnが必要となる。このときの係数 cn、およびφn は下式で与えられる。
![]()
さて、式が続いたので、ここで実際のフーリエ変換の例をとして方形波とインパルス信号を取り上げてみる。なお、計算とグラフ表示はエクセルの機能を使ったもので誰でも簡単に実行できる。
方形波はアンプなどの過渡特性を調べる場合良く使われる波形である。この場合、発信機により作られる波形なので、完全に周期的な信号である。従って、時間窓(周期 T) は1波形の時間をとれば十分である。
フーリエ係数は(2)式により求まるわけであるが、計算は省略し、結果のみ示すと、
an=0, b2n=0, b2n+1=4/(2n+1)π
となる。具体的に(1)式を書けば、
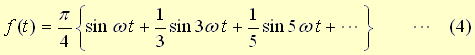
となり、サイン波成分の奇数次高調波の和であらわせる。
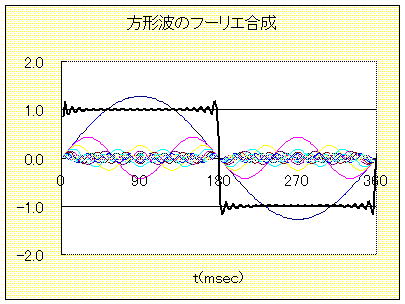
これを、実際に計算してグラフに描いたのが左図である。
この時、周期はT=360msec すなわち、角振動数 ω=17.45 rad/sec, 第43次高調波 (n = 21)まで足し合せた結果である。
黒太線が合成波、黒細線が基底波(n=0)、以下,少しわかりにくいが、高次高調波が色別に描かれている。
理想的な方形波を得るには、さらに高次成分を取り込まなけれなければならない。
すなわち、方形波は非常に高い周波数成分を含み、これをアンプで増幅しようとすると、高い周波数までフラットな周波数特性を持つ必要がある。
瞬間的に発生する直流信号をインパルス信号という。インパルス信号は高調波を同じ強度で含んでおり、例えばスピーカーにインパルス信号を入れ、その応答をコンピュータで解析すると、原理的には、周波数特性のみならず過渡特性なども推定できる。
フーリエ係数は、an=1、bn=0 で、全高調波を同じ強度で含むコサイン波の合成として表せる。
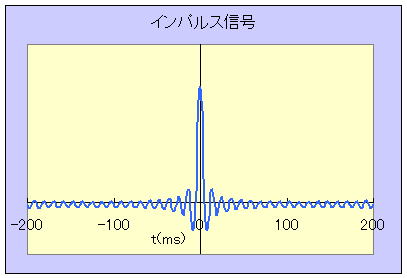
これを、実際に計算してグラフに描いたのが左図である。
この時、周期は時間窓、t1=-125ms、t2=125ms、T=250ms、すなわち、f=4Hz、角振動数 ω=25.13 Rad/s, 第22次高調波 (n = 22)まで足し合せた結果である。
理想的なインパルス信号を得るには、さらに高次成分を取り込まなけれなければならない。
すなわち、インパルス信号は非常に高い周波数成分を均等に含み、これをアンプで増幅しようとすると、高い周波数までフラットな周波数特性を持つ必要がある。
瞬間的に発生する交流信号をトーンバースト信号という。例えば、拍手の音などである。物理学の方では波束とよび、波束の伝播速度を群速度とよぶ。このような信号をフーリエ合成で作るには、中心周波数fc のコサイン波にその周辺の周波数のコサイン波を混ぜることによって可能である。
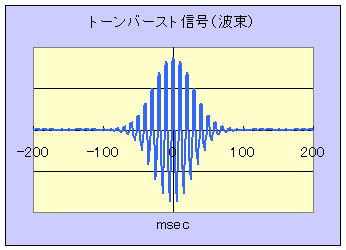
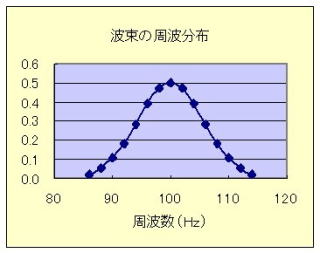
左図は、fc=100Hz を中心に、その周辺 ±10Hz 程度のコサイン波を2Hz置きに右図のようなガウス分布で重みを付け合成した波形である。この時、時間窓は t1= -250ms, t2=250ms, T=500ms, f=2Hz, ω=12.6Rad/s である。
さて、いよいよここで群遅延の説明である。上の波束は、(3)式、すなわち、
![]()
で、φn=0 とした合成波と見做せる。この様な波束をアンプやスピーカーに入れたとき、もし周波数に依存する位相遅れ(又は進み)が生じたらどうなるだろうか?
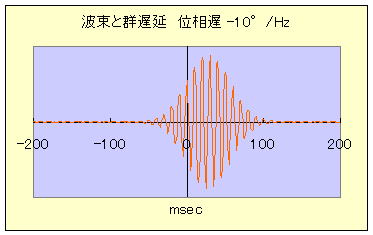
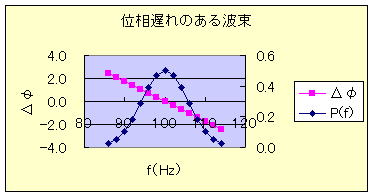
いま、fc(=100Hz)では、位相遅れ無し、すなわち、φ(100Hz)=0 とし、周辺の周波数では、ΔΦ=(f - fc)Δφで表せる位相変化(上図右 ピンク印)があった場合の合成波を計算したのが上図左である。
この時、上右図にしめすように、周波数分布は遅延の無い場合と同じで(上図右 黒丸)、位相遅れはΔφ=-10度/Hz=-0.174Rad/Hz として計算した。
このようにして合成された波束の中心位置(最大振幅の位置)は少し右側(30msecほど時間遅れ側)にずれていることがわかる。
さて、群遅延時間の定義として使われる式、
![]()
で計算すると、Δt=27msとなり、上左図の波束の中心位置のずれと対応している。
この時間遅れがまさに群遅延時間に相当する。
なお、群遅延による時間遅れは決して信号が媒体(電線や空気)を伝わる時間に由来するものでなく位相歪み一つの表現であることに注意する必要がある。また、(5)式の与える群遅延時間は絶対値であり、全周波数範囲にわたってΔt が一定(即ち、位相遅れが周波数に比例して変化する場合)であれば、そこを時間の原点ととればよいわけで、聴感上は時間遅れとして感じない。
群遅延が最も問題になるのはスピーカー、特に低音での特性である。
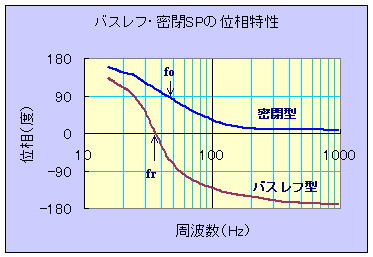 スピーカーシステムを単純にバネと重りで表すモデル(雑学帳 スピーカーの低音再生能力参照)で考えると、ボイスコイルの駆動力に対するコーンの運動は共鳴周波数をはさんで、ゆっくり動かす場合と、高速に振動させる場合で位相が180度異なって来る。さらに、バスレフ型だと2つの共鳴点を持つので360度変化する。この様子を左図に示す。
スピーカーシステムを単純にバネと重りで表すモデル(雑学帳 スピーカーの低音再生能力参照)で考えると、ボイスコイルの駆動力に対するコーンの運動は共鳴周波数をはさんで、ゆっくり動かす場合と、高速に振動させる場合で位相が180度異なって来る。さらに、バスレフ型だと2つの共鳴点を持つので360度変化する。この様子を左図に示す。
foは密閉型のスピーカーユニットの共振周波数。
f rはバスレフ型のポートとコーンの共鳴周波数の中心付近を表す。
なお、位相の絶対値は何処を基準に取るかによるので意味はない。
位相変化の周波数微分値である群遅延時間は当然バスレフ型の方が大きくなる。

左図は、実際のスピーカーシステムにおける群遅延時間の周波数特性を示す。
明らかに、バスレフ型の方が群遅延時間が大きい。最大値はほぼその周波数の1周期に相当する。
それに対し、密閉型の方が群遅延時間がずっと短い。
すこし乱暴だが、このことから密閉システムの方がいわゆる『スピード感のある低音』が得られることが分かる。
なお、人間の聴覚が、どれくらいの群遅延時間を検知出来るかについてはここを参考
ところで、上の例では位相変化は周波数とともに単調に減少する場合であり、群遅延時間は正であったが、もし逆であれば遅延時間が負になり、単純に考えると信号が来る前に音が出るという奇妙な現象が起こることになる。フルレンジスピーカーの位相特性は基本的に単調減少となるがマルチウエイ・スピーカではそうでない。さて、これをどう解釈するか?結構悩ましい問題である。一応ここで筆をおくので皆さん考えてください。
Topへ