(1)狙われる小球が自由落下する場合
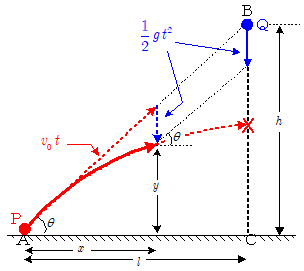
上図のように,点Aより小球Pを初速 $v_0$ ,水平に対する発射角 $\theta$ で発射し,同時に小球Qを前方距離 $l$ ,高さ $h$ の点Bより自由落下させたとして,PとQが衝突する条件について考える。
Pの放物運動において,時間 $t$ 後の水平距離 $x$ ,地面からの高さ $y$ は,重力加速度を $g$ として, \[ \left \{ \begin{array}{rl} & \kern-1em x=v_0\cos\theta\cdot t\\ & \kern-1em \quad=(v_0\times t)* \cos\theta \cdots\maru{1} \\ & \kern-1em y=v_0\sin\theta \cdot t-\bun{1}{2}g\, t^2 \\ & \kern-1em \quad=(v_0\times t )*\sin\theta -\bun{1}{2}g\, t^2 \cdots\maru{2} \end{array} \right . \] 上の $\maru{1}$ 式を見ると,小球Pの時間 $t$ 後の水平方向の変位 $x$ は,初速度 $v_0$ で時間 $t$ だけ等速度運動をしたときの水平距離( $v_0 \, t*\cos\theta$ )に等しく,また $\maru{2}$ 式より,小球Pの時間 $t$ 後の高さ $y$ は,初速度 $v_0$ で時間 $t$ だけ等速度運動をしたときの高さ( $v_0 \, t*\sin\theta$ )から時間 $t$ だけ自由落下した距離($\bun{1}{2}g \,\, t^2$ )を差し引いた値に等しいことがわかる。すなわち放物運動は,初速度 $v_0$ の等速直線運動と自由落下運動を組み合わせた運動とみることができることになる。
一方小球Qは自由落下をしているのであるから,時間 $t$ 間のP,Qの自由落下距離はともに $\color{blue}{\bun{1}{2}g\,\, t^2}$ である。すなわち,PもQも同じ時間内に同じ距離ずつ落下していることになる。したがってもし上図のように,PがQの初期位置Bに向けA→B方向(発射角 $\theta$ が $\tan\theta=h/l$ を満たす向き)に発射されたとすると ,PとQを結ぶ直線はどの時刻においても常に直線ABに平行,すなわち水平に対して $\tan\theta=h/l$ を満たす向きになっており,そしてP・Q間の距離が発射時より $v_0\,\, t$ だけ短くなっていることになる。
このことから,次のことが言える。
もし小球Qとともに運動する観測者がいて小球Pを見ていたとすると,この場合,Pはこの観測者(小球Q)をめがけて直線的に速さ $v_0$ で接近してくるように見えることになるであろう。すなわちQに対するPの相対運動は,水平に対して $\tan\theta=h/l$ を満たす傾き $\theta$ をなす直線上を速さ $v_0$ で運動する等速直線運動(a)として観測されることになる。そしてついに $\overline{\mathrm{PQ}}=0$ となれば,両者は衝突する。
衝突までの時間を $t_0$ とすると, $\overline{\mathrm{PQ}}=0$ より, \[ \overline{\mathrm{PQ}}=0=\overline{\mathrm{AB}}-v_0 \, t_0 \\ \quad\therefore t_0=\bun{\overline{\mathrm{AB}}}{v_0}=\bun{\kon{l^2+h^2}}{v_0} \] さらに両球が空中で衝突する条件は,衝突時におけるQの高さが $0$ 以上であるとおいて, \[ y_\mathrm{Q}=h-\bun{1}{2}g\, t_0{}^2 \ge 0\\ \therefore h-\bun{1}{2}g\bigg(\bun{\kon{l^2+h^2}}{v_0}\bigg)^2 \ge 0\\ \therefore v_0\geqq \kon{\bun{g(l^2+h^2)}{2h} } \] でなければならない。
以下,P・Qの衝突についてまとめると, \[ 発射角:\tan\theta=\bun{h}{l} \quad (\Vvec{AB}の方向)\\ 衝突時刻: t_0=\bun{\kon{l^2+h^2}}{v_0}\\ 空中で衝突する条件:v_0\geqq \kon{\bun{g(l^2+h^2)}{2h} } \] となる。
【参考】P,Qの時刻$t$における位置は, \[ P:\left \{ \begin{array}{rl} & \kern-1em x_\mathrm{P}=v_0\cos\theta\cdot t \\ & \kern-1em y_\mathrm{P}=v_0\sin\theta\cdot t-\bun{1}{2}gt^2 \end{array} \right . \\ Q:\left \{ \begin{array}{rl} & \kern-1em x_\mathrm{Q}=l \\ & \kern-1em y_\mathrm{Q}=h-\bun{1}{2}gt^2 \end{array} \right . \] 衝突するということは,ある時刻においてPとQの位置座標が同じになるということだから,$x_\mathrm{P}=x_\mathrm{Q}$,$y_\mathrm{P}=y_\mathrm{Q}$とおいて, \[ \left \{ \begin{array}{rl} & \kern-1em v_0\cos\theta\cdot t_0=l \cdots\maru{3}\\ & \kern-1em v_0\sin\theta\cdot t_0-\bun{1}{2}g\, t_0{}^2=h-\bun{1}{2}g\, t_0{}^2\\ & \kern-1em \quad\therefore v_0\sin\theta\cdot t_0=h \cdots\maru{4} \end{array} \right . \] $\maru{4}\div\maru{3}$より,$\tan\theta=\bun{h}{l}$ \[\therefore \cos\theta=\bun{1}{\kon{1+\tan^2\theta}}=\bun{l}{\kon{l^2+h^2}}\\ \maru{3}より, t_0=\bun{l}{v_0\cos\theta}=\bun{\kon{l^2+h^2}}{v_0} \]
(2)小球の大きさを考慮する必要がある場合
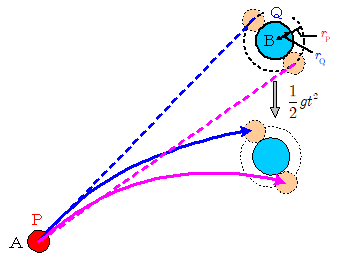
上記下線部(a)で述べたように,Qとともに運動する観測者がPを見た場合,Pは直線的にQに接近してくるように見える。両球の大きさが無視できない場合も,この考え方に立てば,直ちに推測できるであろう。
2球の衝突が起きるためには,2球の表面が接触しあう極限を考えればよいので,上図の青の破線からピンクの破線の間の発射角でPを打ち出せばよい。すなわち,Qの初期位置Bを中心にして,QとPの半径の和( $r_\mathrm{Q}+r_\mathrm{P}$ )を半径とする円内に向けて打ち出せばよい。
青色破線の方向に打ち出した場合は,青色実線で示したようにPはQの上部をかすめるようにすれ違うことになり,ピンク色破線の方向に打ち出した場合は,ピンク色実線で示したようにQの下部をかすめるようにすれ違うことになる。
(3)狙われる小球も初速を持つ場合
お猿さんが木から飛び出した……という場合に相当しますが,上記のように成分分けをした説明では式が煩雑になるので,下記のベクトル表記をした一般的な説明を参照ください。
◎同じ加速度をもつ2物体間の相対運動:
2物体P,Qが同じ加速度 $\Vec{a}$ の等加速度運動をしているとする。P,Qの初期位置を $\Vec{r_0}$ , $\Vec{R_0}$ ,初速度を $\Vec{v_0}$ , $\Vec{V_0}$ とし,時刻 $t$ における位置をそれぞれ $\Vec{r}$ , $\Vec{R}$ とすると, \[\left \{ \begin{array}{rl} & \kern-1em \Vec{r}=\Vec{r_0}+\Vec{v_0}\cdot t +\bun{1}{2}\Vec{a}t^2\\ & \kern-1em \Vec{R}=\Vec{R_0}+\Vec{V_0}\cdot t +\bun{1}{2}\Vec{a}t^2 \end{array} \right . \] よって,Qに対するPの相対的位置 $\Vec{L}$ は, \[ \Vec{L}=\Vec{r}-\Vec{R}\\ \quad =(\Vec{r_0}-\Vec{R_0})+(\Vec{v_0}-\Vec{V_0})\cdot t \] すなわち,相対運動では加速度 $\Vec{a}$ の効果は相殺されてしまい,相対初速度 $\Vec{v_0}-\Vec{V_0}$ なる速度の等速度運動となってしまう。 $\Vec{a}$ を重力加速度 $\Vec{g}$ と考えれば,重力場における2物体の相対運動も同様である。
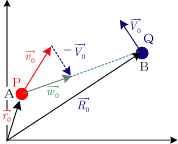
よって上図において,初期時におけるP,Qの位置をA,B,相対初速度を $\Vec{w_0}$ とすると, \[\Vec{r_0}-\Vec{R_0}=\Vvec{BA}=-\Vvec{AB} \\ (or\quad \Vec{R_0}=\Vec{r_0}+\Vvec{AB}) \\ \Vec{w_0}=\Vec{v_0}+(-\Vec{V_0}) \\ (or\quad \Vec{v_0}=\Vec{V_0}+\Vec{w_0}) \\ \therefore \Vec{L}=(\Vec{r_0}-\Vec{R_0})+(\Vec{v_0}-\Vec{V_0})\cdot t\\ \quad= -\Vvec{AB}+\Vec{w_0}\cdot t \] ゆえにPとQが衝突する,すなわち $\Vec{L}=0$ となるには, \[0=-\Vvec{AB}+\Vec{w_0}\cdot t_0\\ \therefore \Vec{w_0}\cdot t_0=\Vvec{AB} \] の関係が成立する必要があり,したがってPの初速度 $\Vec{v_0}$ からQの初速度 $\Vec{V_0}$ を差し引いた相対初速度 $\Vec{w_0}$ がA→Bの方向に向いてかなければならないことがわかる。
そして衝突までの時間 $t_0$ は, \[ t_0=\bun{|\Vvec{AB}|}{|\Vec{w_0}|}=\bun{\overline{\mathrm{AB}}}{\bigg|\Vec{v_0}-\Vec{V_0}\bigg|} \] となる。