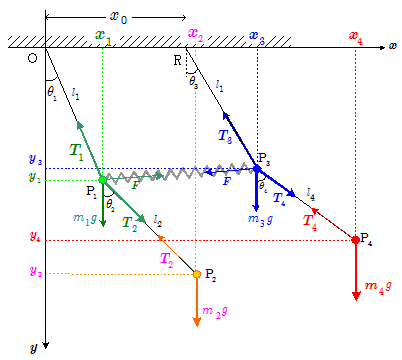
上図において，天井の距離 $x_0$だけ離れた２点Ｏ，Ｒからそれぞれ第１球 $\mathrm{P_1}$（質量 $m_1$），第３球 $\mathrm{P_3}$（質量 $m_3$）が共に長さ $l_1$ の糸（または針金）で吊るされ，その下にそれぞれ第２球$\mathrm{P_2}$（質量 $m_2$），第４球$\mathrm{P_4}$（質量 $m_4$）がそれぞれ長さ $l_2$ ，$l_4$の糸で結ばれているとする。またさらに，第１球 $\mathrm{P_1}$ と第３球 $\mathrm{P_3}$はばね定数 $k$ ，自然長がＯ・Ｒ間の距離に等しい $x_0$ のばねで結ばれている。糸もばねも，その質量は無視できる。
　各小球の座標を図のようにとり，糸の張力を図のように表す。ただし各小球とも変位は十分に小さく，糸が鉛直線となす角 $\theta_1$～$\theta_4$はきわめて小さい値とする。したがって各小球の変位方向は水平方向と近似できるとする。またそれぞれの角 $\theta$ に対して，以下の近似式が適用できるものとする。\[\sin\theta \kinji \theta，　　　\cos\theta \kinji 1 \] このとき $\mathrm{P_1}$ , $\mathrm{P_3}$ 間にはたらくばねの力 $F$ は水平方向にはたらいていると考えてよく，その大きさは，\[F=k(x_3-x_1-x_0)=k\{(x_0 + l_1\sin\theta_3) - l_1\sin\theta_1 - x_0 \} \kinji k(l_1\theta_3 - l_1\theta_1 ) \]である。 　またこの近似が適用できるとき，各小球の変位，加速度 $\bigg(以下，\bun{\mathrm{d^2}x}{\mathrm{d}t^2}=\ddot x 　のように表記する \bigg)$ は以下のように表される。 \[\mathrm{P_1}：\left \{ \begin{array}{rl} & \kern-1em x_1=l_1\sin\theta_1 \kinji l_1\theta_1\quad\quad\therefore \ddot x_1=l_1\ddot {\theta_1}\cdots\cdots\maru{1} \\ & \kern-1em y_1=l_1\cos\theta_1\kinji l_1\quad\quad\quad\therefore \ddot y_1=0\cdots\cdots\maru{2} \end{array} \right . \] \[\mathrm{P_2}：\left \{ \begin{array}{rl} & \kern-1em x_2=l_1\sin\theta_1 + l_2\sin\theta_2 \kinji l_1\theta_1 + l_2\theta_2 \quad\quad\therefore \ddot x_2=l_1\ddot {\theta_1} + l_2\ddot {\theta_2}\cdots\cdots\maru{3} \\ & \kern-1em y_2=l_1\cos\theta_1 + l_1\cos\theta_1 \kinji l_1 + l_2 \quad\quad\quad\therefore \ddot y_2=0\cdots\cdots\cdots\cdots\maru{4} \end{array} \right . \] 　$\mathrm{P_1}$ と $\mathrm{P_3}$ は同じ長さ $l_1$ の糸に結ばれていることに注意して， \[\mathrm{P_3}：\left \{ \begin{array}{rl} & \kern-1em x_3=x_0 + l_1\sin\theta_3 \kinji x_0 + l_1\theta_3\quad\quad\therefore \ddot x_3=l_1\ddot {\theta_3}\cdots\cdots\maru{5} \\ & \kern-1em y_3=l_1\cos\theta_3\kinji l_1\quad\quad\quad\quad\quad\quad\quad\therefore \ddot y_3=0\cdots\cdots\maru{6} \end{array} \right . \] \[\mathrm{P_4}：\left \{ \begin{array}{rl} & \kern-1em x_4=x_0+ l_1\sin\theta_3 + l_4\sin\theta_4 \kinji x_0 + l_1\theta_3 + l_4\theta_4 \quad\quad\therefore \ddot x_4=l_1\ddot {\theta_3} + l_4\ddot {\theta_4}\cdots\cdots\maru{7} \\ & \kern-1em y_4=l_1\cos\theta_4 + l_4\cos\theta_1 \kinji l_1 + l_4 \quad\quad\quad\quad\quad\quad\quad\quad\therefore \ddot y_4=0\cdots\cdots\cdots\cdots\maru{8} \end{array} \right . \] 　よって各球の $x$ 方向， $y$ 方向の運動方程式は， \[\mathrm{P_1}：\left \{ \begin{array}{rl} & \kern-1em m_1\ddot x_1=-T_1\sin\theta_1 + T_2\sin\theta_2 + F \\ & \kern-1em \quad\quad\quad\quad\therefore m_1l_1\ddot \theta_1 \kinji -T_1 \theta_1 + T_2 \theta_2 + k(l_1\theta_3 - l_1\theta_1 )\cdots\cdots\maru{9} \\ & \kern-1em m_1\ddot y_1=-T_1\cos\theta_1 + T_2\cos\theta_2 + m_1g \\ & \kern-1em \quad\quad\quad\quad\therefore m_1\cdot 0 \kinji -T_1 +T_2 + m_1g \cdots\cdots(10) \end{array} \right . \] \[\mathrm{P_2}：\left \{ \begin{array}{rl} & \kern-1em m_2\ddot x_2=-T_2\sin\theta_2 \\ & \kern-1em \quad\quad\quad\quad\therefore m_2(l_1\ddot \theta_1 + l_2\ddot \theta_2) \kinji -T_2 \theta_2\cdots\cdots(11) \\ & \kern-1em m_2\ddot y_2=-T_2\cos\theta_2 + m_2g \\ & \kern-1em \quad\quad\quad\quad\therefore m_2\cdot 0 \kinji -T_2 + m_2g\cdots\cdots(12) \end{array} \right . \] \[\mathrm{P_3}：\left \{ \begin{array}{rl} & \kern-1em m_3\ddot x_3=-T_3\sin\theta_3 + T_4\sin\theta_4 - F \\ & \kern-1em \quad\quad\quad\quad\therefore m_3l_1\ddot \theta_3 \kinji -T_3 \theta_3 + T_4 \theta_4 - k(l_1\theta_3 - l_1\theta_1 )\cdots\cdots(13) \\ & \kern-1em m_3\ddot y_3=-T_3\cos\theta_3 + T_4\cos\theta_4 + m_3g \\ & \kern-1em \quad\quad\quad\quad\therefore m_3\cdot 0 \kinji -T_3 +T_4 + m_3g \cdots\cdots(14) \end{array} \right . \] \[\mathrm{P_4}：\left \{ \begin{array}{rl} & \kern-1em m_4\ddot x_4=-T_4\sin\theta_4 \\ & \kern-1em \quad\quad\quad\quad\therefore m_4(l_1\ddot \theta_3 + l_4\ddot \theta_4) \kinji -T_4 \theta_4\cdots\cdots(15) \\ & \kern-1em m_4\ddot y_4=-T_4\cos\theta_4 + m_4g \\ & \kern-1em \quad\quad\quad\quad\therefore m_4\cdot 0 \kinji -T_4 + m_4g\cdots\cdots(16) \end{array} \right . \] 　(12)より，　　$T_2=m_2g$
　(10)より，　　$T_1=T_2+m_1g=(m_1 + m_2)g$
　(16)より，　　$T_4=m_4g$
　(14)より，　　$T_3=T_4+m_3g=(m_3 + m_4)g$
　以上４式の関係を(9)，(11)，(13)，(15)式に代入して， \[ \kern-1em\left \{ \begin{array}{rl} & \kern-1em (9)より，　　m_1l_1\ddot \theta_1 = -(m_1 + m_2)g\theta_1 + m_2g\theta_2 + k(l_1\theta_3 - l_1\theta_1 )\cdots\cdots(9') \\ & \kern-1em (11)より，　m_2(l_1\ddot \theta_1 + l_2\ddot \theta_2)= - m_2g\theta_2 \cdots\cdots(11') \\ & \kern-1em (13)より，　m_3l_1\ddot \theta_3 = -(m_3 + m_4)g\theta_3 + m_4g\theta_4 - k(l_1\theta_3 - l_1\theta_1 )\cdots\cdots(13') \\ & \kern-1em (15)より，　m_4(l_1\ddot \theta_3 + l_4\ddot \theta_4)= - m_4g\theta_4 \cdots\cdots(15') \\ \end{array} \right . \] 　以上4式を連立させて， \[ \left \{ \begin{array}{rl} & \kern-1em \ddot \theta_1 = \bun{1}{m_1l_1}\big[-\big\{(m_1+m_2)g+kl_1\big\}\theta_1 + m_2g\theta_2 + k l_1\theta_3 \big] \\ & \kern-1em \ddot \theta_2 = \bun{1}{m_1l_2}\big[\big\{(m_1+m_2)g+kl_1\big\}\theta_1 - (m_1 + m_2)g\theta_2 - k l_1\theta_3 \big] \\ & \kern-1em \ddot \theta_3 = \bun{1}{m_3l_1}\big[-\big\{(m_3+m_4)g+kl_1\big\}\theta_3 + m_4g\theta_4 + k l_1\theta_1 \big] \\ & \kern-1em \ddot \theta_4 = \bun{1}{m_3l_4}\big[\big\{(m_3+m_4)g+kl_1\big\}\theta_3 - (m_3 + m_4)g\theta_4 - k l_1\theta_1 \big] \end{array} \right . \] 　この４式をもとにルンゲ・クッタ法で数値解析したのが，本シミュレーションである。

　本シミュレーションでは先に示したような近似を適用しているので，振動を重ねていくうちに誤差が蓄積され，ずれの増大・拡大が起きてきます。この点を承知しておいてください。