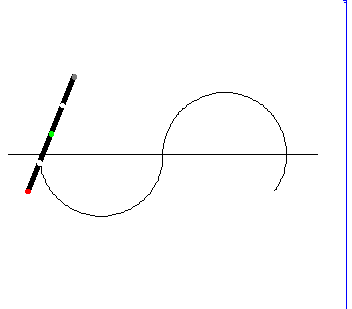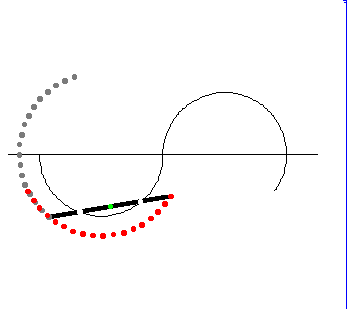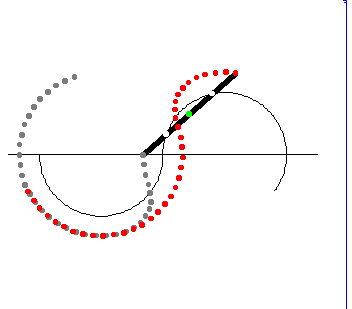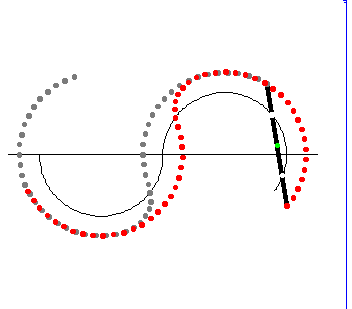
上のアニメは,これを模式化したものです。2つの円形レールの接続部分を電車が通過するとき電車は妙な動きをしていますが,電車の先頭と後部はこのとき激しく揺れます。実はこのとき,電車の自転の仕方が変わる(?)ために揺れるのです。
◎概 要:
カーブしている電車は自転している!?・・・
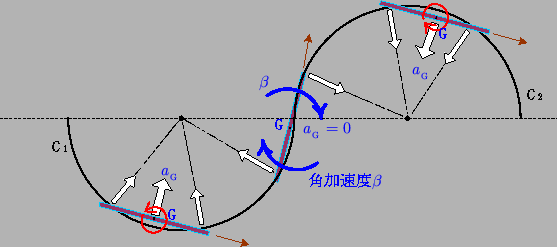
電車がカーブするとき,電車の各部分には向心加速度が作用しています。上図のグレーの矢印で示したのが向心加速度です。
ところがこのほかに大事なことがあります。実はこのとき,電車は自転しているのです。これは,大きさの無視できない電車が前と後ろの2つの 支点(前輪と後輪)をレール上に乗せて,カーブしているレール上を運動(回転運動)していることに起因します。
円形のレール上を電車がぐるぐる回っているとしましょう。このとき電車は,カーブしているとき内側の側面だけを常に円形レールの中心に向けています。これは,お月さんがいつも地球に同じ面を向けているのと同じ理由によります。つまり,お月さんが地球を1周する間にお月さん自身も1回転,自転しているからです。
ところがレールのカーブの向きが逆になると,電車の自転の向きも逆になります。
上図を見てください。下半分のレール $\mathrm{C}_1$ を通過中のとき電車は反時計回りに自転していますが,上のレール $\mathrm{C}_2$ を運動しているとき電車は時計回りに自転しています。
そこで電車が2つのレールの接続部分を通過するとき,電車の自転方向の逆転が起きます。
このことを分かりやすくするために,簡単な場合として,電車の中心Gがちょうど2つのレールの接続部分を通過中としましょう。このとき電車の前輪部分はレール $\mathrm{C}_2$ 上にありますのでその加速度は上図において右向き,後輪部分はレール $\mathrm{C}_1$ にありますからその加速度は左向き,したがって電車の中心Gの加速度 $a_\mathrm{G}$ はゼロになっています。一方このとき,中心G以外のところの加速度は,Gを中心とした自転方向の逆転に伴う角加速度(上図の角加速度 $\beta$ )のみが作用します。この自転角加速度は電車全体で同じですから,この角加速度に中心Gからの距離を乗じた値が電車各点の加速度になります。なので,電車の中心から離れたところほど大きな加速度が働き,大きく揺れるのです。
このようなことが起きるのは,カーブの向きが変わるところ,難しく言うと曲率(曲線や局面の曲がり具合を表す量)が変化するところ(変曲点),たとえば電車が引き込み線から本線に出ようとするときとか,バスがうねうね道を蛇行するようなとき,あるいは一定半径のレール上であっても自転角速度が変わる場合,つまり速さが変わる場合にのみ起きます。
以上が,電車やバスの先頭が揺れやすい原因です。乗り物酔いというのはこの種の揺れも関係していると考えられますので,酔いやすい人はなるべく乗り物の真中付近に乗るのが良いことになります。