放物面鏡による反射については，入試問題にもときどき出題されることがある。
　ここでは，東京農工大の出題例（要旨）をもとに解説します。

　＊＊＊【問題要旨】＊＊＊

(１)

　図１のような凹面鏡ＭＯＮに平面波が入射し，反射後，波がすべて $y$ 軸上の点Ｇ $(\, 0, \, b \,)$ に集まるときの凹面鏡ＭＯＮの形状に関する関数を求める。凹面鏡ＭＯＮは $y$ 軸に関して対称であり，平面波は $y$ 軸に垂直な波面をもって $y$ に沿って入射するものとする。平面波が反射後点Ｇに集まるということは，一つの波面上の各点から出た波は，凹面鏡で反射後，点Ｇに同時に達する，つまり波面上の各点から点Ｇに達する時間が等しいことを意味する。
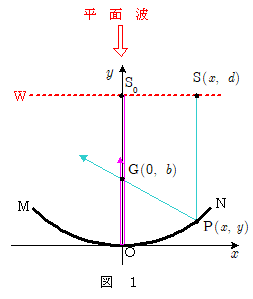
　いま，ある瞬間における一つの波面Ｗ上の点Ｓ $(\, x, \, d \,)$ から出た波が凹面鏡の点Ｐ $(\, x, \, y \,)$ で反射後点Ｇに達する時間 $t$ は，波の速さを $c$ として，　$t=\waku{(ア)}$　である。また，同じ波面Ｗ上の点 $\mathrm{S}_0(\, 0, \, d \,)$ から出た波が$\mathrm{S_0}$→原点Ｏ→Ｇの経路で点Ｇに達する時間 $t_0$ は，　$t_0=\waku{(イ)}$　である。両者を等しいとおくことによって，凹面鏡ＭＯＮの形状に関する式が求まる。凹面鏡ＭＯＮの形状は\[y=\waku{(ウ)}\]を満たす。
(２)

　上記（1）で求めた凹面鏡ＭＯＮが図２のように置かれている。また $y$ 軸上には小さな物体ＡＢが $y$ 軸に垂直に置かれている。物体ＡＢの凹面鏡ＭＯＮによる像を作図する方法について述べよ。ただし，点Ｇ $(\, 0, \, b \,)$ は与えられているものとする。

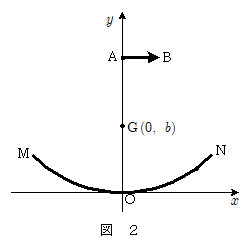
　解　答：

(１)　（ア） \[\kern -1em t=\bun{\overline{\mathrm{SP}}+\overline{\mathrm{PG}}}{c}\\ = \color{blue}{\bun{(d-y) + \kon{x^2 + (b-y)^2}}{c}} \] （イ）\[\kern -1em t_0=\bun{\overline{\mathrm{S_0 O}}+\overline{\mathrm{OG}}}{c}\\ = \color{blue}{\bun{d + b }{c}} \] （ウ）　 $t_0=t$ より，\[\kern -1em \bun{d + b }{c}= \bun{(d-y) + \kon{x^2 + (b-y)^2}}{c}\\ \therefore (b+y)^2= x^2 + (b - y)^2\\ \therefore 2by=x^2 - 2by \\ \therefore \color{blue}{y = \bun{1}{4b}x^2}\quad \cdots\cdots （放物線） \] 　点Ｇは，この放物面の焦点にあたる。すなわち，放物面鏡に中心軸に沿って入射した平面波は，すべて放物面の焦点に収斂すことになる。パラボラアンテナは，この原理を利用して，遠方からの電波（ほとんど平面波となっている）を焦点に置かれた検出器に集めていることになる。
　逆に，焦点の位置から射出された波は，放物面鏡に反射後，平面波となって出ていくことになる。
(２)

　$\maru{\mathrm{a}}$　点Ｂを通り $y$ 軸に平行な光線は，放物面鏡に反射後点Ｇを通る（上図の赤線）。
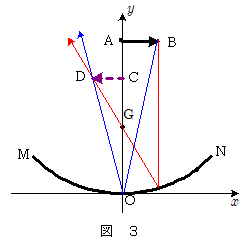
　　$\maru{\mathrm{b}}$　点Ｂを通り原点Ｏに向かった光線は，反射後，対称性により $y$ 軸に関して対称な方向に向かう（上図の青線）。
　以上，２つの光線の交点Ｄの位置に物体ＡＢのＢの像ができるように作図する。

　　　戻る