ブランコ詳解
戻る
分野別一覧へ トップページへ
「ブランコをこぐ」の物理的解説
角運動量の変化量は,力のモーメントに等しい(後述参照)。
(詳細はここをクリック)。
いま図において,質量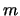 の質点Pが固定点Oのまわりを距離
の質点Pが固定点Oのまわりを距離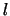 ,角速度
,角速度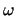 で回転しているとき,質点Pの角運動量は
で回転しているとき,質点Pの角運動量は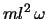 で与えられる。一方質点Pに働く力が点Oのまわりにもつモーメントは,角
で与えられる。一方質点Pに働く力が点Oのまわりにもつモーメントは,角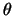 の向き(反時計回り)を正として
の向き(反時計回り)を正として
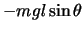 である。よってこのとき次式が成り立つ。
である。よってこのとき次式が成り立つ。
上記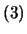 式の
式の
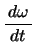 が質点Pの角加速度を与える式で,これに距離
が質点Pの角加速度を与える式で,これに距離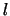 を乗じた値がPの接線加速度を与える。
を乗じた値がPの接線加速度を与える。
ここで大事なのは,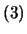 式の第2項
式の第2項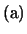 である。もしこの項がなければ,
である。もしこの項がなければ,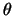 が正の範囲では
が正の範囲では
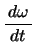 は負,
は負,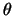 が負の範囲では
が負の範囲では
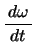 は正となり,質点Pは
は正となり,質点Pは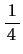 周期ごとに加速されたり減速されたりで,全体としては少しも振れは大きくはなっていかない。
周期ごとに加速されたり減速されたりで,全体としては少しも振れは大きくはなっていかない。
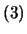 式の第2項
式の第2項 には
には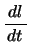 の因子がある。つまり,支点Oからの距離
の因子がある。つまり,支点Oからの距離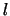 を時間変化させることによって,
を時間変化させることによって,
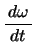 の値を変えることができるのである。「ブランコをこぐ」とは,しゃがんだり立ち上がったりすることによってブランコの支点と人の重心との距離を変え,
の値を変えることができるのである。「ブランコをこぐ」とは,しゃがんだり立ち上がったりすることによってブランコの支点と人の重心との距離を変え,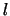 を変化させることなのである。
を変化させることなのである。
そこで,図の
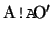 間にあって反時計の向きに回転しているときであれば,
間にあって反時計の向きに回転しているときであれば,
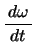 が正であればPは加速されていく。この範囲では
が正であればPは加速されていく。この範囲では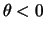 ゆえ
ゆえ
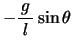 は正で,
は正で,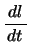 が負,つまり距離
が負,つまり距離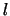 が減少(立ち上がる)すれば第2項
が減少(立ち上がる)すれば第2項 は正となり,
は正となり,
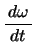 は全体として正となり,質点Pは加速される。その値は
は全体として正となり,質点Pは加速される。その値は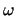 が大きaいときに
が大きaいときに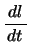 が大きければよい。つまり,下方に達したときほど急速に
が大きければよい。つまり,下方に達したときほど急速に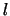 を小さく(急速に立ち上がる)していけばよい。
を小さく(急速に立ち上がる)していけばよい。
つぎに最下点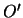 を越えて上昇していく場合を考える。この場合はPは減速されていくが,
を越えて上昇していく場合を考える。この場合はPは減速されていくが,
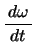 の絶対値がなるべく小さければ減速のされ方が小さくて,より高いところに達することができるようになる。
の絶対値がなるべく小さければ減速のされ方が小さくて,より高いところに達することができるようになる。
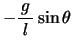 は負であるから,第2項
は負であるから,第2項 が正であれば
が正であれば
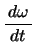 の絶対値を小さくできる。そのためにはやはり
の絶対値を小さくできる。そのためにはやはり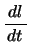 が負であればよい。つまり距離
が負であればよい。つまり距離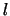 を小さく(立ち上がる)していけばよいことになる。
を小さく(立ち上がる)していけばよいことになる。
そして最高点にったっしたところでしゃがみ,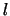 を大きくする。このとき
を大きくする。このとき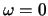 ゆえ,第2項
ゆえ,第2項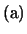 の効果は
の効果は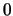 である。
である。
以上より,ブランコを効率良くこぐには,上でしゃがみ,下で立ち上がるのがよい。
質量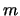 の物体の位置
の物体の位置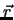 での速度が
での速度が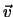 であるとき,
であるとき,
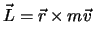 なる物理量をこの物体の角運動量という。角運動量の時間微分をしてみると,
なる物理量をこの物体の角運動量という。角運動量の時間微分をしてみると,
ここで2つのベクトルの積
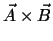 をベクトルの外積(ベクトル積ともいう)といい,その大きさ
をベクトルの外積(ベクトル積ともいう)といい,その大きさ
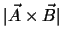 は,2つのベクトルの互いに直角な成分同士の積である。したっがて,同じ2つのベクトルの外積は
は,2つのベクトルの互いに直角な成分同士の積である。したっがて,同じ2つのベクトルの外積は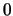 となるので,
となるので,
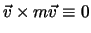 、したがって上式右辺第1項は0である。また,
、したがって上式右辺第1項は0である。また,
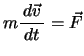 であるから,上式は
であるから,上式は
なる関係が導かれる。
ここで角運動量の大きさ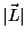 は,
は,
ただし,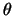 は
は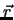 と
と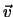 とがなす角である。ここで,
とがなす角である。ここで,
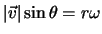 であることから,
であることから,
となり,さきの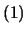 式が得られる。また,
式が得られる。また,
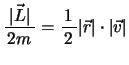 となり,これは上図斜線部の面積に等しく,これを面積速度という。角運動量は面積速度を2倍して質量をかけた量であるから,角運動量が保存されるとき面積速度も一定に保たれる。これを面積速度一定の原理という。
となり,これは上図斜線部の面積に等しく,これを面積速度という。角運動量は面積速度を2倍して質量をかけた量であるから,角運動量が保存されるとき面積速度も一定に保たれる。これを面積速度一定の原理という。
![\includegraphics[scale=1.2]{buranko_kaisetu1-1.eps}](img1.gif)
![\includegraphics[scale=1.2]{buranko_kaisetu1-1.eps}](img1.gif)
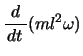
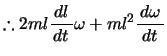
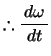
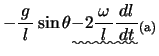
![\includegraphics[scale=1]{buranko_kaisetu22-1.eps}](img25.gif)
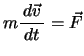 であるから,上式は
であるから,上式は
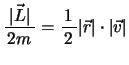 となり,これは上図斜線部の面積に等しく,これを面積速度という。角運動量は面積速度を2倍して質量をかけた量であるから,角運動量が保存されるとき面積速度も一定に保たれる。これを面積速度一定の原理という。
となり,これは上図斜線部の面積に等しく,これを面積速度という。角運動量は面積速度を2倍して質量をかけた量であるから,角運動量が保存されるとき面積速度も一定に保たれる。これを面積速度一定の原理という。