気体分子運動にみる断熱変化
戻る ビジュアル物理へ トップページへ
入試問題で出題される代表的な気体分子運動論を例として、以下に解説する。
断面積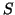 のシリンダー内に
のシリンダー内に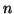 モルの単原子分子(1分子の質量が
モルの単原子分子(1分子の質量が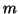 )の理想気体が、ピストンで封入されている。はじめシリンダーの長さは
)の理想気体が、ピストンで封入されている。はじめシリンダーの長さは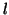 で、気体の温度は
で、気体の温度は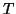 、圧力は
、圧力は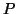 とする。ピストンに垂直な方向を
とする。ピストンに垂直な方向を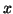 軸とする。分子とピストンとの衝突は弾性衝突とし、分子どうしの衝突はないとする。
軸とする。分子とピストンとの衝突は弾性衝突とし、分子どうしの衝突はないとする。
ある分子がピストンに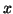 軸方向の速度成分
軸方向の速度成分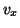 で衝突とすると、
で衝突とすると、
この分子がピストンに与える力積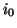 は、
は、
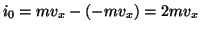
この分子とピストンとの単位時間あたりの衝突回数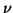 は、
は、
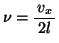
この分子が単位時間にピストンに与える力積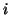 は、
は、
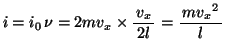
全分子の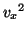 の平均を
の平均を
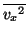 とすると、全分子からピストンが単位時間に受ける力積
とすると、全分子からピストンが単位時間に受ける力積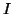 は、アボガドロ数を
は、アボガドロ数を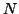 、
、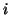 の平均を
の平均を
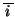 として、
として、
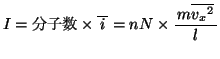
また、分子運動に方向の偏りがないこと(分子運動の等方性)から、
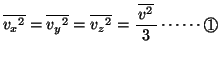
さらに力積と運度量変化との関係
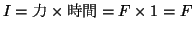 であることとから、
であることとから、
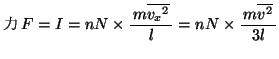
よって圧力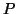 は、力
は、力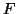 を面積
を面積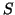 で割って、
で割って、
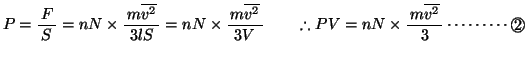
ここで、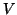 は体積である。一方、気体の状態方程式から、
は体積である。一方、気体の状態方程式から、
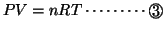
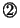 と
と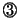 とより、
とより、
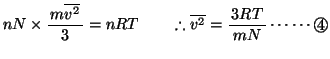
ここで理想気体の内部エネルギーは気体分子の運動エネルギーの和であるから、単原子分子の場合、
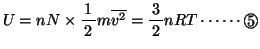
(2原子以上からなる分子の場合は、これに分子自身の回転のエネルギーが加わるので、内部エネルギーは上記の値より大きくなる。)
つぎに、ピストンを移動させて、気体を断熱的に膨張させる場合を考える。
![\begin{wrapfigure}[9]{r}{20zw}
\includegraphics[scale=.8]{fig2-2.eps}\end{wrapfigure}](img33.gif)
ピストンの移動速度を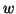 とすると、ピストンと衝突した分子の速度の
とすると、ピストンと衝突した分子の速度の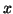 方向成分は
方向成分は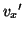 は、ピストンとの衝突が弾性的であることから、はねかえり係数の式を使って、
は、ピストンとの衝突が弾性的であることから、はねかえり係数の式を使って、
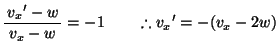
よって1回の衝突による運動エネルギーの増加
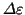 は、
は、
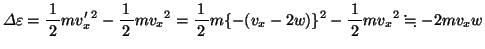
ただし、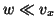 として
として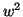 の項は省略した。またこのことから、単位時間あたりのピストンとの衝突回数は近似的に
の項は省略した。またこのことから、単位時間あたりのピストンとの衝突回数は近似的に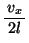 と考えていいので、ピストンが距離
と考えていいので、ピストンが距離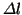 移動する時間
移動する時間
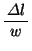 の間の衝突回数
の間の衝突回数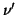 は、
は、
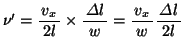
よってこの間のこの分子の運動エネルギーの増加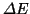 は、
は、
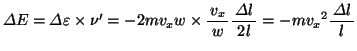
全分子による運動エネルギーの和、つまり内部エネルギーの増加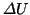 は、
は、
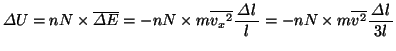
ここで 式を利用した。体積増加
式を利用した。体積増加
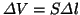 であるから、
であるから、
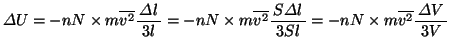
上式に 式を代入して、
式を代入して、
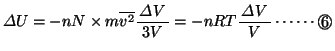
一方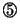 式より、
式より、
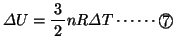
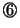 式と
式と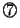 式とより、
式とより、
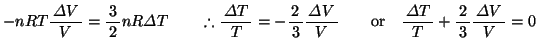
上式から得られる式を積分して、
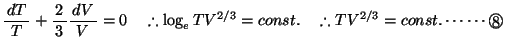
このように、一般に理想気体が断熱的に変化をするとき、温度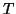 と体積
と体積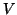 との間に
との間に
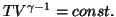 という関係が成立する。さらにこの式にボイル・シャルルの法則
という関係が成立する。さらにこの式にボイル・シャルルの法則
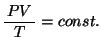 を乗ずると、
を乗ずると、
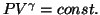 を得る。ここで
を得る。ここで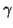 は比熱比と呼ばれる定数で、定圧比熱と定積比熱の比
は比熱比と呼ばれる定数で、定圧比熱と定積比熱の比
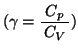 である。これらの断熱変化で成り立つ関係式を
である。これらの断熱変化で成り立つ関係式を
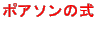 という。
という。 式は単原子分子の場合のポアソンの式で、
式は単原子分子の場合のポアソンの式で、
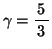 の場合にあたる。なお、先のアニメーションのおいて、グラフに示した理論値とはこの
の場合にあたる。なお、先のアニメーションのおいて、グラフに示した理論値とはこの 式を示している。
式を示している。
![\begin{wrapfigure}[10]{r}{20zw}
\includegraphics[scale=1]{fig1-1.eps}\end{wrapfigure}](img1.gif)
![\begin{wrapfigure}[10]{r}{20zw}
\includegraphics[scale=1]{fig1-1.eps}\end{wrapfigure}](img1.gif)
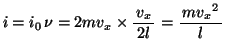
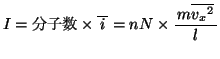
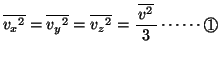
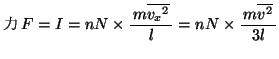
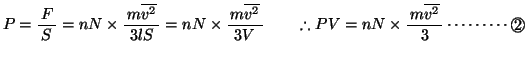
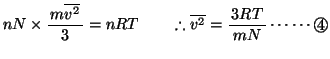
![\begin{wrapfigure}[9]{r}{20zw}
\includegraphics[scale=.8]{fig2-2.eps}\end{wrapfigure}](img33.gif)
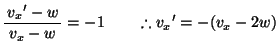
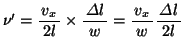
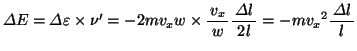
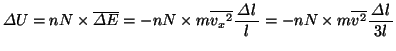
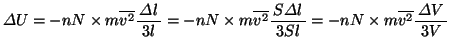
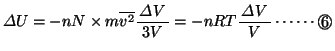
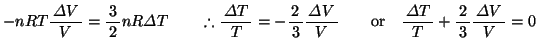
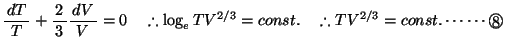
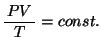 を乗ずると、
を乗ずると、
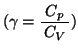 である。これらの断熱変化で成り立つ関係式を
である。これらの断熱変化で成り立つ関係式を