円形波の干渉と干渉条件

戻る　　 分野別一覧へ　　　　　トップページへ

　

１．行路差による干渉条件

　

　

\includegraphics[scale=1.2]{setumei-1-1.eps}
　
　上図において、$S_1$、$S_2$は振動数$f$の点波源で、これらを中心に波長$\lambda$の円形波が広がっているとする。このとき、$S_1$、$S_2$からそれぞれ距離$l_1$、$l_2$ずつ離れた点Ｐにおいてこれら２波源からの波が強め合うか弱め合うかを考える。
　$l_1>l_2$と仮定する。$S_1$、$S_2$からは次々と波が送り出されている。ある時刻に、$S_1$、$S_2$から同時に出発した波の山「１」のうち、$S_2$からの山「１」が点Ｐに届いたとき、もし $l_1-l_2=\lambda$であったとすると、$S_1$からの波の山「１」は点Ｐより$\lambda$だけ手前の点Ｑの位置にある。したがってその１周期後に点Ｑにあった$S_1$からの山「１」が点Ｐに達し、このとき$S_2$からの山「２」が点Ｐに届く（１周期分先行）ので、点Ｐでは$S_1$、$S_2$からのともに「山」が重なることになり、２つの波は強め合う。一般に、 $l_1-l_2=n\lambda \quad(n:整数)$ならば、点Ｐにおいて$S_1$からの山「１」は$S_2$からの山「$n$」と出会い（$n$周期分先行）、２つの波は強め合う。これは谷同士で考えても同じことである。
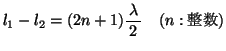　しかしもし $l_1-l_2=0.5\lambda$だったとすると、$S_1$からの山「１」が点Ｐに達したとき$S_2$からの谷「１'」がＰに届くので、２つの波は弱め合うことになる。一般に、 $l_1-l_2=(2n+1)\bun{\lambda}{2}\quad(n:整数)$ならば、点Ｐにおいて$S_1$からの山「１」は$S_2$からの谷「$n'$」と出会い、２つの波は弱め合うことになる。
　また、もともと$S_1$、$S_2$間に$\pi$の位相差がある場合、$S_1$から「やま」が出ていくとき$S_2$からは「谷」が出ていくので、上記の関係は逆になる。以上より、干渉条件は以下のようにまとめられる。。
　---------------------------------------
1゜　$S_1$、$S_2$に位相差がないとき：

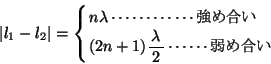
\begin{displaymath} \vert l_1-l_2\vert= \left\{ \begin{array}{rl} \!\!\!\!\!\!... ...bun{\lambda}{2} \cdots\cdots 弱め合い \\ \end{array} \right. \end{displaymath}

2゜　$S_1$、$S_2$に$\pi$の位相差があるとき：

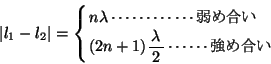
\begin{displaymath} \vert l_1-l_2\vert= \left\{ \begin{array}{rl} \!\!\!\!\!\!... ...bun{\lambda}{2} \cdots\cdots 強め合い \\ \end{array} \right. \end{displaymath}

　---------------------------------------
　

２．節線について

　

\includegraphics[scale=0.7]{setumei-3.eps}
\includegraphics[scale=0.7]{setumei-3.eps}
２つの点波源から送り出されていく円形波が干渉すると、かなり複雑な波紋ができる。この様子の一例を上のアニメで示してある。このとき、全く振動しない点（振幅０の点）を結んだ線を $\textcolor{red}{節線（せっせん）}$という。節線は双曲線もしくは直線をなす。以下にこれを示す。
上図のように、節線上の１点をＰとする。このとき節線上では振幅が０であるから、先に述べた干渉条件の式を使うと、次のようになる。ただし、ここでは２波源$S_1$、$S_2$は同位相で振動しているとする。

\begin{displaymath}\vert \overline{\mathrm{S_1P}}-\overline{\mathrm{S_2P}} \vert=(2n+1)\bun{\lambda}{2} \end{displaymath}

１本の節線はある同じ$n$に対する弱め合いの点を結んだ線であるから、１本の節線上では$S_1$、$S_2$からの距離に差が一定値をとる。２点からの距離差が一定値をとる曲線は双曲線か直線である。
では次に、節線が何本できるかを考える。$S_1$、$S_2$からの円形波を直線 $\mathrm{S_1S_2}$上で見ると、この直線上では$S_1$、$S_2$からの波が逆向きに進んでくるので、この線上には定常波ができている。節線は振幅０の点を結んだ曲線であるから、当然直線 $\mathrm{S_1S_2}$にできる定常波の節の位置を通っているはずである。したがって節線の数は、直線 $\mathrm{S_1S_2}$にできる定常波の節のかずに等しい。つまり節線が何本できているかは、直線 $\mathrm{S_1S_2}$にできる定常波の図を描いてみて、その節の数を数えればよいことになる。
節線数 $= \mathrm{S_1S_2}$上にできる定常波の節の数