enkeiha-syoukai

円形波の干渉　詳解

$\includegraphics [scale=1]{setumei-3-1.eps}$

　上図において、 $\mathrm{S_1}$ 、 $\mathrm{S_2}$ は振動数の点波源で、これらを中心に波長 $\lambda$ の円形波が広がっているとする。このとき、 $\mathrm{S_1}$ 、 $\mathrm{S_2}$ の振動が、それぞれ

$\begin{eqnarray*} y_{\mathrm{S_1}} &=& a \sin 2\pi f t \\ y_{\mathrm{S_2}} &=& a \sin (2\pi f t + \delta) \quad (\delta:位相差) \end{eqnarray*}$

と表されるとき、 $\mathrm{S_1}$ 、 $\mathrm{S_2}$ からそれぞれ距離

、

離れた点Ｐにける振動は次のようになる。

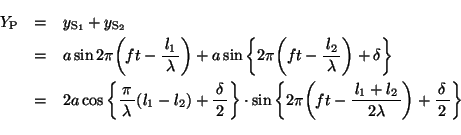
$\begin{eqnarray*} Y_\mathrm{P} &=& y_{\mathrm{S_1}}+y_{\mathrm{S_2}} \\ &=& a ... ...(f t-\bun{l_1+l_2}{2\lambda} \bigg)+\bun{\delta}{2} \bigg \} \\ \end{eqnarray*}$

上式の第２項（第２因子）は時刻

を含んでおり、この項は点Ｐが振動数

で振動することを表す振動項である。そして第１項（第１因子）の絶対値が、点Ｐの振動振幅

を表す。

$\begin{displaymath} A = 2a \bigg \vert \cos \bigg \{ \bun{\pi}{\lambda}(l_1-l_2)+\bun{\delta}{2} \bigg \} \bigg \vert \end{displaymath}$

(1)

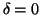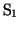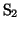　 $\delta=0$ 、したがって $\mathrm{S_1}$ 、 $\mathrm{S_2}$ が同位相で振動している場合：

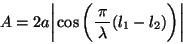
$\begin{displaymath} A = 2a \bigg \vert \cos \bigg ( \bun{\pi}{\lambda}(l_1-l_2) \bigg ) \bigg \vert \end{displaymath}$

よって

を整数として、

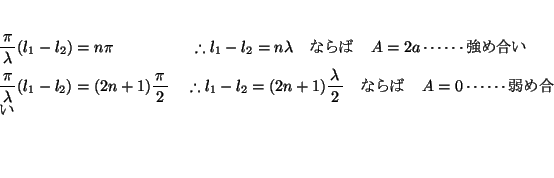
$\begin{eqnarray*} % latex2html id marker 53\bun{\pi}{\lambda}(l_1-l_2) &=& n ... ...bun{\lambda}{2} \quad ならば \quad A=0 \cdots\cdots 弱め合い \\ \end{eqnarray*}$

(2)

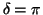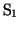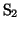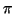　 $\delta=\pi$ 、したがって $\mathrm{S_1}$ 、 $\mathrm{S_2}$ が位相差 $\pi$ で振動している場合：

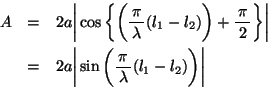
$\begin{eqnarray*} A &=& 2a \bigg \vert \cos \bigg \{ \bigg ( \bun{\pi}{\lambda}(... ... \sin \bigg ( \bun{\pi}{\lambda}(l_1-l_2) \bigg ) \bigg \vert\\ \end{eqnarray*}$

よって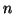

を整数として、

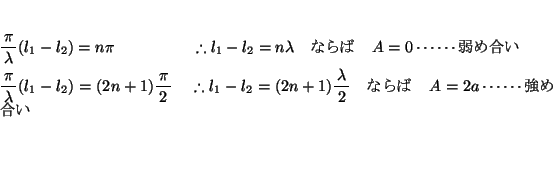
$\begin{eqnarray*} % latex2html id marker 73\bun{\pi}{\lambda}(l_1-l_2) &=& n ... ...un{\lambda}{2} \quad ならば \quad A=2a \cdots\cdots 強め合い \\ \end{eqnarray*}$

以上が、行路差による干渉条件式である。この関係式は、光波による干渉を考える場合もそのまま適用できる。

　次に節線について考える。上述したように、点Ｐにおける振幅は $\mathrm{S_1}$ 、 $\mathrm{S_2}$ からの距離差によって決まる。したがってが同じ値なら振幅も同じ値になるわけで、同じ振幅の点はそれぞれ双曲線か直線になることが分かる。