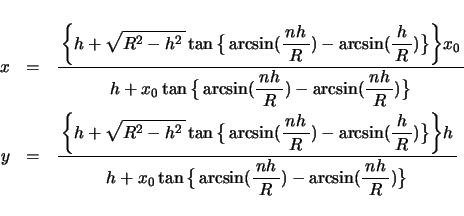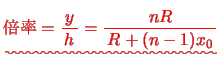上図において,球の中心を通る直線①と,物体の上端Pから出て光軸 に平行に進む光線②との交点として像の位置を求める。
に平行に進む光線②との交点として像の位置を求める。
物体の 座標を
座標を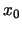 ,物体の高さを
,物体の高さを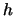 とすると,光線①は屈折しないので,光線①は
とすると,光線①は屈折しないので,光線①は
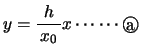 なる式で表される。
なる式で表される。
つぎに光線②について考える。球形容器の半径を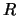 ,容器内の屈折率を
,容器内の屈折率を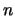 ,外の屈折率を
,外の屈折率を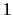 とし,また各部分の角度を図のように設定すると,点Qにおける屈折の法則は,
とし,また各部分の角度を図のように設定すると,点Qにおける屈折の法則は,
ここで
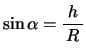 であるから,
であるから,
一方点Qの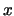 座標
座標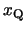 は
は
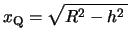 であるから,屈折後の光線②は次式で表される。
であるから,屈折後の光線②は次式で表される。
 に
に を代入して
を代入して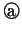 式と
式と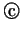 式とを連立させて
式とを連立させて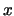 ,
,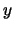 を求めると,
を求めると,
となる。ここで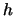 が
が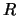 に比べて十分に小さくしたがって光軸
に比べて十分に小さくしたがって光軸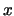 軸に近い光線のみを考えてよいとすると,以下の近似式を適用して,
軸に近い光線のみを考えてよいとすると,以下の近似式を適用して,
よって倍率は
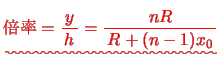
となって,金魚の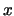 座標が小さい,すなわち眼から遠ざかるほど倍率は高くなり,金魚は大きく見えることになる。たとえば水の屈折率はおおよそ
座標が小さい,すなわち眼から遠ざかるほど倍率は高くなり,金魚は大きく見えることになる。たとえば水の屈折率はおおよそ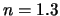 ぐらいであるから、金魚が金魚鉢の中心付近にいれば
ぐらいであるから、金魚が金魚鉢の中心付近にいれば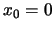 とおいて倍率は
とおいて倍率は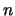 に等しく
に等しく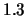 倍、もっとも遠い位置にいるとして
倍、もっとも遠い位置にいるとして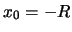 とすると倍率は
とすると倍率は
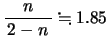 倍となる。
倍となる。
![\includegraphics [scale=1]{kingyo-kaisetu-1.eps}](img1.gif)
![\includegraphics [scale=1]{kingyo-kaisetu-1.eps}](img1.gif)
![]() に平行に進む光線②との交点として像の位置を求める。
に平行に進む光線②との交点として像の位置を求める。
![]() 座標を
座標を![]() ,物体の高さを
,物体の高さを![]() とすると,光線①は屈折しないので,光線①は
とすると,光線①は屈折しないので,光線①は
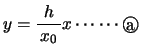 なる式で表される。
なる式で表される。
![]() ,容器内の屈折率を
,容器内の屈折率を![]() ,外の屈折率を
,外の屈折率を![]() とし,また各部分の角度を図のように設定すると,点Qにおける屈折の法則は,
とし,また各部分の角度を図のように設定すると,点Qにおける屈折の法則は,
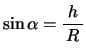 であるから,
であるから,