
ハイジの歌声

![]()
|
◎相等単振り子 ロープの重さも考慮する今回のような「実体振り子」は、 下に示す長さの「相等単振り子(ロープの重さ=0とした振り子)」に置き換えて考えることができる。 相等単振り子の長さ:L' = I/(M・h) I : 実体振り子の慣性モーメント = Σmi・Xi^2 M : 実体振り子の総重量 h : 実体振り子の支点〜重心の長さ = (Σmi・Xi)/M 計算すると、 L' =(Σmi・Xi^2)/(Σmi・Xi) =(2∫mr・dx・x^2+Mh・L^2)/(2∫mr・dx・x+Mh・L) ↑ロープ左右2本分として2倍 積分(∫)範囲:0〜L = L・(2・mr・L+3・Mh)/(mr・L+Mh)/3 mr : ロープ単位長さあたり重さ Mh : ハイジ体重+ロープ結び目重さ L : ロープ長さ(ブランコ支点〜ブランコ椅子までの長さ) ⇒ 以下、長さL'の単振り子の運動として考える。 ◎ブランコの運動 さて、ブランコの運動を考えるにあたって、Jacobiの積分はさっさとあきらめて、以下の漸化式で解くことにする。 (これならEXCELでできるのだ。) |
| t | φ(t) | θ1(t) | 重心の速度 Vr(t) | 重心の加速度 a(t) |
| 0 | 0 | 1(0)=-70゚ | 0 | -g・sin(-70゚) |
| 1 | -(g・sinθ1(0)・Δt^2)/2/L' | θ1(0)+φ(1) | a(0)・Δt | -g・sinθ1(1)-k・Vr(1)^2 |
| 2 | -((g・sinθ1(1)・Δt^2)/2+Vr(1)・Δt)/L' | θ1(1)+φ(2) | Vr(1)+a(1)・Δt | -g・sinθ1(2)-k・Vr(2)^2 |
| : | : | : | : | : |
| t | -((g・sinθ1(t-1)・Δt^2)/2+Vr(t-1)・Δt)/L' | θ1(t-1)+φ(t) | Vr(t-1)+a(t-1)・Δt | -g・sinθ1(t)±k・Vr(t)^2 |
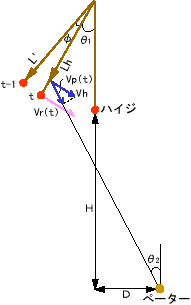
| [補足] t : 時間。時間の刻み幅をΔtとしたとき、n・Δtのnの値。 φ,θ1 : 角度(下図参照) Vr,a : 実体振り子(ブランコ)重心の速度、加速度 (向きはロープと垂直) g : 重力加速度 = 9.8m/sec^2 k : 空気抵抗係数 (抵抗が結構大きそうなので、速度の二乗に比例する ものとする) |
| ◎ペーター方向の速度成分
というわけで、ハイジのブランコの速度Vr(t)が時間の関数として求まった。 「聞こえる歌の音程」を考えるとき、重要なのは「音源から観測者の方向への速度成分」である。・・・これをVp(t)とする。 ブランコに対するペーターの位置を図のD、Hで表すとして、Vpを求めると、 |Vp(t)| = Vh・sin(|θ1|+|θ2|) Vh : ハイジの(口の)位置での速度 ブランコ支点〜ハイジまでの長さを Lhとすると Vh = Lh/L'・Vr θ2 : 角度(図参照) θ2 = arctan((Lh・sin(θ1-D)/ (Lh・(1-cosθ1)+H+Lh)) (幾何学的に考えるために絶対値をとっているが、実際は位置関係によって符号が変わる。) |
 |
| ◎歌の音程変動 さて、いよいよ大詰め、音程についての考察である。 ここで、かのドップラー効果の登場だっ! ドップラー効果の一般式は、 ν' = ν/(1-v/c) ここで、 ν' : 観測される周波数 ν : 音源の周波数 v : 音源と観測点の相対速度 (近づく場合+,遠ざかる場合-) c : 音速 気温T(℃)のとき c =(331.5+0.61・T) 今回、前項で求めた Vp(t) が上記の v に相当する。 従って、音源(ハイジ)の音程(周波数ν)と観測者(ペーター)に聞こえる音程(周波数ν')は以下の関係で与えられる。 ν'/ν =(1-Vp(t)/c) ところで知られているとおり、1オクターブで周波数は2倍となる。 1オクターブの間に半音(12個)が均等な比率で収まっているとする場合(平均率)、隣り合う全音(1オクターブに6個)の周波数の比を r とすると、 ν+ = 2・ν = r^6・ν ⇒ r = 2^(1/6) ν+ : ある音程(周波数ν)の1オクターブ上の周波数 また、周波数比ν'/νのとき音程が n 音ずれるとすると、 ν' = r^n・ν これより、 n = 6・log 2(ν'/ν) そう、この n こそが求めようとしていた「ハイジの歌の音程ずれ」なのでした!や〜れやれ。 何か疑問、質問ある方・・・こちらもあんまり自信ないんで、どうかご自分で解決なさってして下さいませ! m(_ _)m |