マクドナルドで,SNOOPY World Tour をやっている.ご存じスヌーピーが,世界の民族衣装姿を披露する.1998年 12月 17日〜1999年 1月 13日までの 28日間に,28種類のスヌーピーが登場するという.
香港では,毎日一種類ずつ,日替わりだったそうだ.だから,28日間毎日ハッピーセットを一つずつ買えば,すべて揃う.28日間毎日ハンバーガーを食べ続けるのは拷問に近いが,それでも目標は手の届く範囲にある訳だ.
ところが,日本国内では,中の見えない袋に入って,ランダムにプレゼントされる.香港の日替わり方式と違って,種類毎の廃棄がないので,無駄がない.しかし,中のスヌーピーがどんな民族衣装を着ているか,開けるのが楽しみではあろうが,既に揃えたものと同じであればがっかりすることになる.かくして,子供にせがまれた母親は,栄養バランスを気にし,女子高生は体重を気にしながらのチャレンジが続く,そしてマクドナルドの売り上げは伸びる...
*
それでは 28種類のスヌーピーを揃えるには,一体幾つのハンバーガーを食べねばならないのだろうか.
もし 2種類(A, B とする)しかないのなら,計算は簡単である.
| 所用個数 | 確率 |
|---|---|
| 2個 (A または B)(他の種類) | (2/2)(1/2) |
| 3個 (A または B)(同じ種類)(他の種類) | (2/2)(1/2)(1/2) |
| 4個 (A または B)(同じ種類)(同じ種類)(他の種類) | (2/2)(1/2)(1/2)(1/2) |
| ・・・ | ・・・ |
| n個 (A または B)(同じ種類)が(n-2)回(他の種類) | (2/2)(1/2)n-2(1/2) |
であるから,
所用個数の平均
=Σn=2∞ n(2/2)(1/2)n-1
=Σn=2∞ n(1/2)n-1
=2Σn=2∞ n(1/2)n
=2(Σn=1∞ n(1/2)n - 1/2) (Σn=1∞ n xn = x/(1-x)2 は,数学公式集参照)
=2(4-1/2)
=3
3個(=種類の数×1.5)である.
4種類の場合でも,もう少し手間を掛ければ,
所用個数の平均
=Σn=3∞ n((3/3)(2/3)(1/3)Σi=0n-3 (1/3)(n-3)-i(2/3)i)]
=11/2
5.5個(=種類の数×1.8)と計算できる.
| 28 | 1 |
| 29 | 27 |
| 30 | 378 |
| 31 | 3,654 |
| 32 | 27,405 |
| 33 | 169,911 |
| 34 | 906,192 |
| 35 | 4,272,048 |
| 36 | 18,156,204 |
| 37 | 70,607,460 |
| 38 | 254,186,856 |
| … | ・・・ |
しかし,28種類の場合をまともに手計算するのは気が遠くなる.計算式をプログラムしても,なお厄介である.極めて幸運で 28個買うだけで揃う場合は,当然(順序を別にして)一通りしかない.29個を要する場合は,27通りである.しかし,ダブリが 10個,つまり 38個買わねばならないケースは,254,186,856通りにもなるのである.こういう種類の計算の困難さを,組み合わせ的爆発という.
しかし,こんなとき,役に立つのがシミュレーションである.そこで,早速プログラムを書き,シミュレートしてみた結果をグラフにしたのが,下図である.(「シミュレートしてみた」と曖昧な書き方をしたのは,使用した乱数の検定など,このシミュレーションに偏りがないかを調べていないからである.当たらずと雖も遠からず,と思って見て欲しい.)
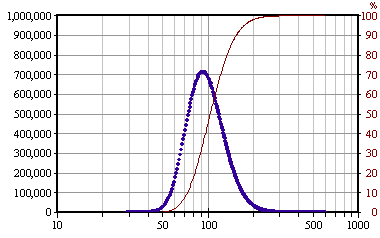
図は,28種類のスヌーピーを全て集めるために必要としたハッピーセットの購入数の,5000万回のシミュレーションを表したグラフである.購入数を表す横軸は,対数目盛になっているので注意.この種の現象では,大概,グラフは左右対称にはならず,右の方に緩やかな裾を引き,対数目盛で数字の大きい方を圧縮すると正規分布に近づき対称性が良くなる,ということが多い.
図中の釣り鐘型をした青い線は,シミュレートされた購入数の実数である.一番多いのは,揃えるまでに,91個必要としたケースであり,5000万回中 713,145回であった.平均は,110個.これは,種類の数 28 の約 4倍に達する.ついでに,標準偏差は,右に ×(4/3),左に ×(3/4) である(対数目盛なので,比率で表した).
一方,茶色の線で表した,中央付近でぐっと立ち上がったグラフは,28種類を全て手に入れた累積の割合で,右目盛りである.このグラフから,104個買うと半数のケースで全種類揃い,154個買えば 90%のケースで揃うことが読み取れる.(半値の位置が 104 と,平均の 110 からずれている.このことから,この分布が正規分布から若干ズレていることが分かる.)
*
これらの数字からすると,日本と香港でスヌーピー人気が同じ程度だとすれば,同じプレゼントを使っても,そのやり方の違いから,日本では香港の数倍の効果があることになろうか.さて,実績はどうなることだろう.
<後日談> (2003年 3月 10日)
2000年 11月 7日に Ma_Ts さんから,メールを戴いた.その一部を以下に引用する.
期待値だけならもっと簡単に解けるのではないでしょうか。
確率 p の現象がおきるまで独立試行を繰り返し、それが起こるまでの回数の期待値を N とすると、一回外れたあとの期待値は N+1 になるので
N=p+(1-p)(N+1)
N=1/p
28種類のスヌーピーをそろえるには、28回"新しい"スヌーピーを当てればいいので k 種類持っているときの新しいのが当たるまでの購入回数の期待値は1/((28-k)/28)=28/(28-k)
その合計は
27
Σ(28/(28-k))≒109.96
k=0
ぴったり同じですね。
全く,その通りである(ご指摘ありがとうございました).と,これだけでは,身も蓋もないので,ついでに,なぜ簡単に計算ができるのか,少し考えてみよう.
情報科学では,トレードオフ(12の基本概念の一つ)という現象をよく目にする.例えば,導入経費を安くあげると維持経費が嵩むといったように,あちらを立てればこちらが立たないことを言う.
上の例における N の等式は,級数の和を求めるときによく使われる,級数の収束を前提とする計算法と同じものである.つまり,上記の N の等式は本当に収束することまでは保証してくれない.収束するとすればこの値になる,ということだけを言っているのである.また,この計算で得られるのは平均値のみであり,分布まではわからない.
つまり,得られる情報量の差が計算量の差になっているのである.
因みに,逐次検定法で必要とする標本数が少なくてすむのも,それによって得られる情報量の差によるものと解することができる.