(G4)において t を変えながら、x を横軸に、y を縦軸にとった x-y 平面での `y(x)` を描いた
グラフ（軌道）は左図の通りである。
曲線の色は、`x_0, y_0` のそれぞれ異なる組に対応している。
こんなところにも微分方程式
作成日：2020-02-15
最終更新日：
2019 年の末から 2020 年の初めにかけて、新型コロナウイルスが話題に上っている。 この関連で、感染症についての簡単な微分方程式を考えたいと思った。 以下の記述は、佐藤 總夫による 自然の数理と社会の数理 II （以下、本書）に基づく。
感染症のモデルを考える。全住民は (n+1) 人として、出入りはないものとする。 伝染病の流行が始まる時間を t = 0 とする。 t = 0 の時点で、n 人の感受性者（ susceptible 、 未感染者でこれから感染を受ける者、感受性保持者ともいう）と 1 人の感染者 ( infected )がいるとする。 時間 t において、感受性者の数を x(t) 、感染者の数を y(t) とおく。 なお、通常のモデルでは、死亡する者や免疫を持った者、隔離された者 （これらをまとめて除去者または免疫保持者という。英語では recoverd または removed ） を別に設け考慮するが、最初のこの単純モデルでは考慮しないものとする。 この除去者があるモデルは後ほど考慮する。 また、x(t) と y(t) はいずれも t について微分可能とする。これらを場合により単に x, y と記す。
まず初期条件から、次の式が成り立つ：
(S1) `x + y = n + 1`
次に、Δ t 時間内に新たに発生する感染者数は、x と y の積に比例すると仮定する。 この理由は、外界と閉ざされた全住民のなかで、交流が均等であればあるほどますます感染しやすい、 という常識から裏付けられる。また、 x + y = n + 1 という条件で、 x と y の積が最も大きいのは x = y のときであるということも考慮する。さて、 この仮定に基づいて次の式が立てられる。
(S2) `(Delta x)/(Delta t) = - beta x y`
ここで、`beta` は(感染|接触)率と呼ばれる正の定数である。右辺にマイナスがあるのは、 左辺である感受性者は時間の経過とともに減っていくからである。
さて、`beta` を推定することは難しいので、ここで新たな変数 u を導入する。 変数 u は時間に関する変量であり、
(S3) `u = beta t`
である。以降の方程式は、`t` についての微分方程式から `u` についての微分方程式に変換する。 `beta` を 1 としても同じようであるが、別のモデルで `beta` を使うことがあるから、 名目上は `beta` を生かしておく。さて、このときの微分方程式は次のようになる：
`(dx)/(du) = (dx)/(dt) (dt)/(du) = 1/beta (dx)/(du) = -xy` 。
微分方程式 (S2) は、上式の変換を使うと、(S1) から、
(S4) `(dx)/(du) = -x(n + 1 - x)`
のように書き換えられる。この式と、初期条件
(S5) `x(0) = n`
を満たす (S4) の解 x(u) を求めれば、感受性者数 x と感染者数 y の時間変化がわかる。さて、(S4) を次のように書き換える：
(S6) `x' + (n+1) x = x^2`。
ここで、
`x' = (dx)/(du)`
である。以下、ダッシュ(') は u に関する微分を表わす。 (S6) の微分方程式はベルヌーイ型と呼ばれる。
さて、(S6)を `x^2` で割ると、
(S6') `(x')/x^2 + (n+1)/x = 1`
が得られる。ここで、
(S7) `z = 1/x`
という置き換えを導入すると、
`z' = (dz)/(du) = (dz)/(dx) (dx)/(du) = -1/x^2 (dx)/(du)`
であるから、これら z と z' の式を (S6') に代入すると、
(S8) `z' - (n+1)z = -1 `
となる。ここで、上記の等式の両辺に `exp(-(n+1)z)` を乗じると、
`z' exp(-(n+1)z) - (n+1)z exp(-(n+1)z) = -exp(-(n+1)z)`。
ここで左辺は `(z exp(-(n+1)z)'` に等しいので、両辺を積分して、
`exp(-(n+1)z) = (exp(-(n+1)z))/(n+1) + C`
を得る。ここで C は積分定数である。上式で u = 0 とおけば、(S5) と (S7) から
`z(0) = 1/(x(0)) = 1/n`
であるから、積分定数 C は、
`C = 1/n - 1/(n+1) = 1/(n(n+1))`。
したがって、`z(u)` の式は、
`z(u) = 1 / (n+1) + (exp((n+1)u)) / (n(n+1))`
となり、`x(u)` に直すと、
(S9) `x(u) = (n(n+1))/(n+exp((n+1)u))`
となる。これより、時刻 u での感染者数 y(u) として、
(S10) `y(u) = n + 1 - x = n +1 - (n(n+1))/(n+exp((n+1)u)) = ((n+1)exp((n+1)u))/(n+exp((n+1)u)) = (n+1)/(1 + n exp(-(n+1)u))`
が得られる。これは、ロジスティック曲線である。
(S10) 式は感受性者数の式である。私たちの関心は、感受性者数というより感染者数であり、 さらには感染者数の増加率である。感染者 y の増加率は感受性者 x の減少率でもあるから、
`(dy)/(du) = -(dx)/(du)`
となる。したがって、新しい感染者の発生率を w(u) で表わすことにすれば、
(S11) `w(u) = -(dx)/(du) = (n(n+1)^2 exp((n+1)u))/({n+exp((n+1)u)}^2)`
が得られる。
`u` を横軸に、`w` を縦軸にとった`u-w` 平面に `w(u)` を描いた曲線を、 流行曲線と呼ぶ。単純モデル(S11)の流行曲線を左図に描いた。 曲線の色が青、緑、橙、赤のそれぞれが `n=10, 20, 30, 40` に対応している。
この流行曲線は、 関数グラフ描画スクリプト・SVGGraph.js http://defghi1977.html.xdomain.jp/tech/SVGGraph/SVGGraphDemo.htm#c を用いて描いた。SVGGraph.js の作者 DEFGHI1977@xboxlive 氏に感謝する。 スクリプトは次の通りである。
setRange(-0.2,0.8,-50,450);
axis('full',0.1,50,0,0);
style.strokeWidth = 3;
style.stroke = 'blue';
plot('10*11*11*e^(11*x)/((10+e^(11*x))^2)');
style.stroke = 'green';
plot('20*21*21*e^(21*x)/((20+e^(21*x))^2)');
style.stroke = 'orange';
plot('30*31*31*e^(31*x)/((30+e^(31*x))^2)');
style.stroke = 'red';
plot('40*41*41*e^(41*x)/((40+e^(41*x))^2)');
流行曲線の性質は次の通りである。
単純モデルでは、死亡者、免疫者、隔離者を無視していた。一般モデルでは、 これらをひとまとめにして除去者 (removed または recoverd）という第三のグループで考える。 すなわち、病気に感染した死亡した者、回復して免疫を持つ者、 隔離されて感染しない者を合わせて除去者という。 このモデルでは、感受性者 (susceptible)、感染者（infected）、除去者(removed) の３グループを考えることから SIR モデルと呼ばれる。
このときのモデル、病気に感染した場合、感受性者は直ちに感染者に変わるものと仮定する。 つまり、潜時は無視できるものとする。
さて、ある地域に住む n 人の集団のうち、ある時点での感受性者数を x(t)、感染者数を y(t)、除去者数を z(t) とする。 単純モデルと同様に、x, y, z は共に t で微分可能とする。また、
(G1) `x + y + z = n`
である。ここで下記を仮定する：
この結果一組の微分方程式を得る：
(G2) `{( (dx)/(dt)=-betaxy),((dy)/(dt)=betaxy - gammay),((dz)/(dt)=-gammay):}`
ここで `beta` は(感染|接触)率、`gamma` は除去率と呼ばれる。また、G-1 の微分方程式は、 (カーマック|ケルマック)-マッケンドリック (Kermack-McKendrick) のモデルと呼ばれる。
伝染病の流行が始まる時点を t = 0 とする。ここで次のように記号を決める：
(G3) `x(0) = x_0, y(0) = y_0, z(0) = 0`
`x_0` と `y_0` はともに正の数である。また、`z(0) = 0` としたのは、 流行が始まるその瞬間に除去者はいないためである。
(G2)の第１式と第２式はともに `z` を含まない。したがって、x, y については、 次の微分方程式
(G4) `{( (dx)/(dt)=-betaxy),((dy)/(dt)=betaxy - gammay = beta y (x-rho)):}`
だけ考えればよい。ただし、`rho = gamma / beta ` である。この `rho` は重要な役割を果たす。
(G4)の第２式を第１式で割ると、
(G5) `(dy)/(dx) = (beta xy - gamma y)/(- beta xy) = -1 + rho / x`
が得られる。これは変数分離型であるから、次のように式を変形して、
`dy = -dx + rho (dx)/x`
両辺を次のように積分できる：
`int_0^t dy = - int_0^t dx + rho int_0^t (dx)/x`。
積分を実行して、次の式が得られる：
`y - y_0 = -x + x_0 + rho (log x - log x_0)`。
移項して式を整えると次の式を得る：
(G6) `y(x) = y_0 + x_0 - x + rho log(x/x_0)`
(G6) のグラフを書いてみよう。(G6) の両辺を x で微分して、
`y'(x) = -1 + rho / x`
が得られる。この式から、`0 < x < rho` では y は x の増加関数であり、 `` では y は x の減少関数であることがわかる。また、
`y''(x) = - rho / x^2 < 0`
であるから、x > 0 の全域にわたって y(x) のグラフは上に凸である。
さらに、(G6)から `y(x_0)=y_0 > 0` であり、
`lim_(x->+0) y(x) -> -oo`
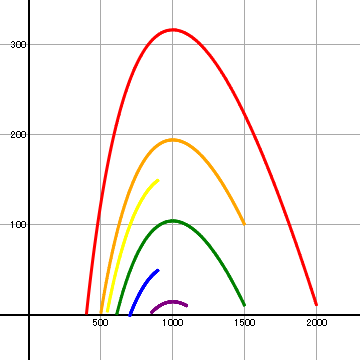
(G4)において t を変えながら、x を横軸に、y を縦軸にとった x-y 平面での `y(x)` を描いた
グラフ（軌道）は左図の通りである。
曲線の色は、`x_0, y_0` のそれぞれ異なる組に対応している。
| 色 | x0 | y0 |
|---|---|---|
| 赤 | 2,000 | 10 |
| 橙 | 1,500 | 100 |
| 黄 | 900 | 150 |
| 緑 | 1,500 | 10 |
| 青 | 900 | 50 |
| 紫 | 1,100 | 10 |
このグラフにおいても、前のグラフと同様、 関数グラフ描画スクリプト・SVGGraph.js http://defghi1977.html.xdomain.jp/tech/SVGGraph/SVGGraphDemo.htm#c を用いて描いた。SVGGraph.js の作者 DEFGHI1977@xboxlive 氏に感謝する。 スクリプトは次の通りである。
setRange(-200,2300,-50,350);
axis('full', 500, 100, 0, 0);
style.strokeWidth = 3;
style.stroke = 'red';
plot('10+2000-x+1000*log(x/2000)', 400, 2000);
style.stroke = 'orange';
plot('100+1500-x+1000*log(x/1500)', 500, 1500);
style.stroke = 'yellow';
plot('150+900-x+1000*log(x/900)', 545, 900);
style.stroke = 'green';
plot('10+1500-x+1000*log(x/1500)', 610, 1500);
style.stroke = 'blue';
plot('50+900-x+1000*log(x/900)', 700, 900);
style.stroke = 'purple';
plot('10+1100-x+1000*log(x/1100)', 850, 1100);
第一象限内の任意の点から出発する(G4)の軌道は、 すべての `t ge 0` にたいして第一象限内にとどまる。 そして、`t -> +oo `のとき、点 (x(t),y(t)) は、 区間 (0, ρ) のなかの一点に収束する。
図から読み取れることは、伝染病の流行は感染者数 y0 の影響よりは、 むしろ感受性者数 x0 の影響が強い、ということである。 そして、x0 < ρ ならば y0 がかなり大きな値でも流行は起きないが、 x0 > ρ ならば y0 がかなり小さな値でも流行は起きる。 そこで、ρ は閾値（いきち）と呼ばれる。
さて、流行の激しさを定量的に表すにはどうしたらよいだろうか。 一つの目安は次の式で与えられる：
`I_rho = (x_0 + y_0 - x_oo)/x_0`
ここで、
`x_oo = lim_(t->+0) x(t)`。
この式の意味は次の通りだ。
`rho` の値を変えてみて、`rho lt x_0` である場合の (G4) のグラフを描き、 それぞれの `I_rho` を求める（表略）と、`rho` の値が大きくなると `I_rho` の値が小さくなることがわかる。
ρ の値が小さいということは、(感染|接触)率 β が大きいか、または除去率 γ が小さいことを意味する。 前者は人口密度が高いことを意味している。 また後者は誤診による病気の見落としや医療制度の不十分性などが考えられる。 このような場合は、Iρ は大きくなる。
一方 ρ の値が大きいということは、(感染|接触)率 β が小さいか、または除去率 γ が大きいことを意味する。 これは先ほどの ρ が小さいことの裏返しであり、 前者は人口密度が低いことを意味している。 また後者は感染症に対する適切な施策や医療制度の十分な整備などが考えられる。 このような場合は、Iρ は小さくなる。
なお、流行最終期における感受性者数 `x_oo = lim_(t->+0) x(t)` の値を計算上得る方法については、 次項の閾値定理を述べたあとで説明する。
前項では、伝染病が流行するか否かの指標として、閾値 `rho = gamma / beta` を示した。 この閾値について、本書（pp.185-pp.187）にしたがって考える。 まず、本書によれば、次の結果が知られている：
感受性者からなる集団に感染者が入っても、感受性者の人口密度がある値を超えない限り、 伝染病の爆発的な流行は起こらない。 しかし、このある値を超えると、爆発的に流行し、 感受性者の密度を閾値より小さな値へと減少させてしまう。
この結果は、カーマックとマッケンドリックによって明らかにされた。
閾値定理を定量的に述べると次のようになる。
初期感受性者を x0、閾値を ρ で表わし、x0 > ρ とする。 ν を正の数として x0 = ρ + ν をおくと、最終的にその病気にかかる住民の数は、 近似的に 2ν に等しくなる。言い換えれば、 流行に初期に閾値 ρ を超えていた感受性者のレベル x0 = ρ + ν は、 流行の最終期には閾値よりも下のレベル x0 - 2ν = ρ - ν まで引き下げられる。
閾値定理の導出は次の通りである。おおまかにいえば、下記の諸量に関する近似が成り立つ場合に、 テイラー展開等を用いて近似するものである。
まず、G6 の式で、`t -> oo` とすれば、
`0 = y_0 + x_0 - x_oo + rho log (x_oo/x_0)`
を得る。ここで、`x_oo = lim_(t->oo) x(t) `とする。
この右辺を `f(x)` とする。今、第１の近似から、
`f(x) ~= x_0 - x_oo + rho log (x_oo/x_0)`
= `x_0 - x_oo + rho log((x_0 - (x_0 - x_oo))/(x_0))`
= `x_0 - x_oo + rho log(1 - (x_0 - x_oo)/(x_0))`
と書ける。ここで、`h` が微小量であるときの log に関するテイラー展開の結果
`log(1+h) ~= h - 1/2 h^2`
を使うとさらに式変形を進めて、
`f(x) ~= x_0 - x_oo - rho ((x_0-x_oo)/x_0) - rho / 2 ((x_0-x_oo)/x_0)^2`
`=(x_0-x_oo)(1- rho/x_0 - rho/(2x_0^2) (x_0 - x_oo))`
`f(x) = 0`かつ、`(x_0-x_oo) != 0` であるから、次が成り立つ：
`1- rho/x_0 - rho/(2x_0^2) (x_0 - x_oo) = 0`
よって
`x_0-x_oo = 2x_0(x_0/rho - 1)`。
`x_0 = rho + nu` を代入して、
`x_0 - x_oo = 2nu + 2 rho (nu/rho)^2`
ここで第３の近似により、第２項を無視すると次の式が得られる：
`x_0-x_oo ~= 2nu`。
この閾値定理がどの程度の誤差で当てはまっているかは次の表を参照してほしい。
流行の最終期における感受性者数 `x_oo` の計算方法について述べる。 これは本書には記載されていないので、私 (MARUYAMA Satosi) による追記である。
`x_oo`は次の式を満たす：
`x_oo = x_0 + y_0 + rho log (x_oo/x_0)`
そこで、
`f(x) = x_0 + y_0 - x + rho log (x/x_0)`
とおき、f(x) = 0 を満たす解 `x = x_oo` を、逐次近似によって見出すことにする。 逐次近似としてはニュートン・ラフソン法を用いる。すなわち、 ｎ回めの近似で得られた解を `x^((n))` とすると、n+1回めの近似解 `x^((n+1))` を
`x^((n+1)) = x^((n)) - f(x^((n)))/(f'(x^((n))))`
で得るものである。なお、
`f'(x) = -1 + rho / x`
である。ここで２つの疑問が生じる：
まず第１の点に関しては、前項の閾値定理で得られた概算数を使えばよい。 すなわち、 `x^((0)) = x_0 - 2ν = x_0 - 2(x_0 - ρ) = 2ρ - x_0 `とすればよい。
次に第２の点に関しては、`f(x)` が上に凸であることから、 `x^((0)) le x_oo` であれば収束する。 `x^((0)) gt x_oo` であっても、`x^((1)) lt x_oo` であるから、 以降逐次近似を実施すれば収束する。
簡単な計算結果を図示する。`x^((i))` 以外は本書p.179の表 1 流行の激しさと同じである （ただし、本書の ρ = 5,000 の場合の `x_0` は6,500 となっているが これは誤りと判断したので、`x_0`を5,500 に直した。 `x^((i)) (i = 0, 1, 2, 3) `については、 小数点以下第３位以降を四捨五入して表示した。
この `x^(oo)` の収束はかなりよいと思う。その上で、本書にある `x_oo` について、
註 `x_oo` は小数第１位を切捨てた数値である．
と付されている。
これについては、私の収束計算結果から、「切捨てた」ではなく「四捨五入した」ではないか、
との疑いを持っているが、さすがに私も正確な計算をしたわけではないので、
これ以上は追究しない。
なお、計算に当たっては JavaScript を使った。
JavaScript による四捨五入については、
別の四捨五入とコンマ区切りを見てほしい。
右２列は、閾値定理の妥当性を検証するための値である。閾値定理によれば、 2ν ≒ x0 - x∞ であるから、かなりのρであてはまっているといえる。 また、この閾値定理は、x∞を数値計算で逐次近似で求めるために、 最初の近似解として妥当であることは、さきに確かめた通りである。
G2 に戻って、除去者数の変化 `(dz)/(dt)` を知るにはどうしたらよいか。 厳密解は求められないので、近似式を求めるしかない。その方法を本書にしたがって述べる。
まず、`x(z)`は厳密解が得られる：
`x(z) = x_0 exp(-z/rho)`
この式と G1 から `(dz)/(dt)` については次の式が得られる：
(A1) `(dz)/(dt) = gamma (n - z - x_0 exp(-z/rho))`
この式の解析解を得るのは難しい。
そこで、次のテイラー展開を利用して、高次の項を切り捨てて近似解を得ることにする。
`exp(-z/rho) ~= 1 - z/rho + 1/2(-z/rho)^2`
途中の導出はばっさり省略して、近似解 `z(t)` について次の式を得る：
(A2) `z(t) = rho^2/x_0 {(x_0/rho - 1) + lambda tanh ((gamma lambda)/2 t - mu) }`
ただし、`mu = tanh^-1 (1/lambda (x_0 / rho - 1))` である。
(A2) で ` t->oo ` を考えると、次の式が得られる：
`lim_(t -> oo) z(t) = z_oo = rho^2/x_0 {(x_o / rho - 1) + lambda}`
ここで、
`lambda = root()((x_0/rho - 1)^2 + (2x_0(n-x_0))/rho^2)`
ここで根号の第２項が第１項より無視できるほど小さいとすれば、近似的に次が成り立つ：
`lambda = x_0/rho - 1`
これを z_oo の式に代入して、次が得られる。
(A2) `z_oo = (2rho^2)/x_0 (x_0/rho - 1) = 2rho(1 - rho/x_0)`
特に、流行が起きるときは `rho lt x_0` であるから、`nu` を正の数として、
`x_0 = rho + nu`
とおくことができる。このとき、
`z_oo = 2rho (1 - rho / x_0) = 2(x_0 - rho) rho / x_0`
となり、x0 が ρ の十分近くにあれば `rho/x_0` はほとんど 1 に近い値をとると考えられる。 したがって、近似的に下記が成り立つ。
(A3) `z_oo = 2nu`
ただしこの結果は、x0 が ρ よりかなり大きな値となるときは使えないことに注意すべきである。
また、この近似解による流行曲線 `(dz)/(dt)` の式は次のようになる：
`(dz)/(dt) = (gamma rho^2 lambda^2)/(2x_0) sech^2 ((gamma lambda)/2t - mu)`
このグラフは、直線 `t = 2 mu // gamma lambda` について対称であることがわかる。
D. G. ケンドールは、一般モデルにおける微分方程式の近似解を求めるのではなく、 微分方程式そのものから流行曲線に関する正確な情報を引き出した。以下この解析法を、 本書（pp.197-pp.203）にしたがって考える。
なお、ケンドールという名前を聞いて、 ひょっとして待ち行列におけるケンドールの記法を思い出した人がいるかもしれない。 佐藤の本で、このケンドールの解析のもとになった論文として掲げているのが、 David G. Kendall であるし、またケンドール記法の創始者も David George Kendall であるから、 同一人である可能性は高いといえる。
ケンドールは、モデルにおいて感染率 β を z の関数であると仮定した。 このときの(G2)のモデルは次の通りとなる。
(K1) `{( (dx)/(dt)=-beta(z)xy),((dy)/(dt)=beta(z)xy - gammay),((dz)/(dt)=-gammay):}`
第１式と第３式から
`(dx)/(dz) = - (beta(x))/gamma x`
`(dx)/x = - 1/gamma beta(z) dz`
`log x = - 1/gamma int_0^z beta(w)dw`
`x = x_0 exp(- 1/gamma int_0^z beta(w)dw)`
したがって、流行曲線は次の式となる：
(k2) `(dz)/(dt) = gamma {n - z - x_o exp(-1/gamma int_0^z beta(w)dw)}`
`beta` を `z` の関数として表現したことで、一つの結果がわかる。 それは、`beta` を特定の `z` の関数として表現して積分計算を実行することで、 カーマックとマッケンドリックの近似モデルは、 感受性者数の減少率を控えめに評価していることがわかる、というものだ。 もちろん、近似モデルにおいては `beta` が一定のもとでモデルを構築しているのだが、 近似を進める仮定において、結果として `beta` が感染者数 `z` の増加につれて減少する、 という効果をもたらしていることがわかる。
流行曲線の式は次の通りであった：
(A1) `(dz)/(dt) = gamma (n - z - x_0 exp(-z/rho))`
この式を t について解くと次の式が得られる。
(K3) `t = 1/gamma int_0^z (dw)/(n - w - x_0 exp(-w/rho))`
この A1 と K3 の式自体から、流行曲線のもつ性質を考える。 ただし、この式では t ≧ 0 という制約があり、解析が困難となる（理由は本書を参照のこと）。 そのため、時間の原点を `x = rho` に移動させることで解析をつづけることができる。 この時点は流行の中心と呼ばれ、流行がもっとも激しくなる時点である。 `x` については次のようにおく：
(K4) `x(0) = x_0 = rho`
このとき、`z` は次のように表わせる：
(K5) `z(0) = z_0 = 0`
したがって、`z(t)` は次の意味を持つ：
(K4), (K5) と 条件 `x_0 + y_0 + z_0 = n` より `n = y_0 + rho` と表わせる。 このとき、A1 と K3 はそれぞれ次のように書き換えられる。
(K6) `(dz)/(dt) = gamma (y_0 - z + rhoexp(-z/rho))`
(K7) `t=1/gamma int_0^z (dw)/(y_0 - w + rho (1 - exp(-w/rho)))`
変数の範囲は次の通りである：
`-oo lt t lt oo, -zeta_1 lt z lt -zeta_2`
ここで `-zeta_1` と `zeta_2` はそれぞれ、方程式
`y_0 - zeta + rho (1 - exp(-zeta/ rho)) = 0`
のただ一つの負の根とただ一つの正の根である。
ここで重要なことは、時間の原点を移動させたことで、 流行の全過程を最初から区間 `(-oo, oo)` に存在する一つのものとして考える、ということである。
導出は省略するが、 `zeta_1` は時間区間 `(-oo, 0)` で生じる除去者の総数を、また `zeta_2` は時間区間 `(0, oo)` で生じる除去者の総数を表わす。 そして、 `(0, oo)`は、 それぞれ区間 `(-oo, 0)` 、`(0, oo)` の流行曲線の下の面積を表わす。
注意すべきことは、一般には `zeta_1 != zeta_2` なので、 流行曲線はカーマックとマッケンドリックの近似解とは異なり、 対称軸を持たない。
流行曲線の非対称性と流行の強さにはどのような関係があるか、本書にしたがって述べる。
まず、近似モデルにおける住民総数に相当する量を確認する。
詳細は省略して、結果のみ記す。全住民数に相当する数は `x_(-oo) = lim_(t->-oo) x` とする。
この値を `N` とする。この `N` は次のように表わされる:
`N = x_(-oo) = rho + y_0 + zeta_1`
この `N` を用いて、流行の強さ `I` を次の式で定義する：
`I = (zeta_1 + zeta_2)/N`
`t -> 0` のとき、`t=0` のとき、`t -> oo`のときの諸量は次のようになる。
| t | -∞ | 0 | ∞ |
|---|---|---|---|
| x:感受性者 | N | ρ | N-NI |
| y:感染者 | 0 | y0 | 0 |
| z:除去者 | -ζ1 | 0 | NI-ζ1 |
モデルの諸量の計算過程を省略し、次の式が得られる。
次の段階は、 全住民相当数 `N` と閾値 `rho` の比 `N/rho` を流行の強さ `I` で表わすことである。ここでは `I` として、 `N` に対する除去者総数 `z_oo - z_-oo = zeta_2 + zeta_1` の割合と定義する。すなわち、
`I = (zeta_1 + zeta_2) / N`
さて、`N/rho` は次の式で与えられる。
(K8) `N/rho = - (log(1-I))/I`
途中の導出を省略し、 流行前後の除去者数の割合の非対称性を表す数値を `zeta_1 / (zeta_1+zeta_2)` とすると、
`zeta_1 / (zeta_1+zeta_2) = 1/I (N/rho)^-1 log{:N/rho:}`
さらに途中の導出を省略し、`t = 0`における感染者数 `y_0` は `N` 、`rho` を使って次のように表わされる。
`y_0 / N = 1 - (N/rho)^-1 (1 + log {:N/rho:})`
なお、上式は、本書の p.206 の (31) 式であるが、 本書の (31) 式は log の符号がマイナスになっていて、これは誤植である。上式が正しい。
さて、モデル G2の数値例の一部を取り出すと次の通りである。
表 モデルの数値例
このことから、通常は流行の中心以後に発生する除去者数の割合のほうが、 中心以前に発生する除去者数より多いことがわかる。
上記の表が得られたとき、本書では特に、`N//rho gt 4` の場合に注目している(pp.207-208)。
このとき、次の数値が提示されている：
`zeta_1 / (zeta_1+zeta_2) lt 0.3536, zeta_2 / (zeta_1 + zeta_2) lt 0.6464`
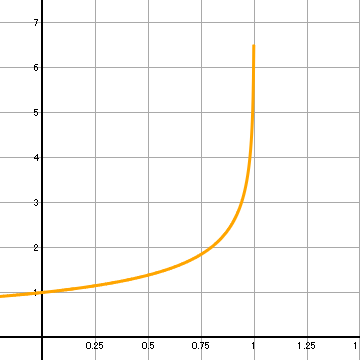
これは上記の表にはない。`N//rho = 4` のときの `I` が求まって初めて `zeta_1 / (zeta_1+zeta_2)` が求められる。さて、横軸を `I` にとって、 縦軸に `N//rho` をとったグラフを書いてみよう。 三たび 関数グラフ描画スクリプト・SVGGraph.js によるグラフを使うと次のようになる。 このグラフからわかることは、`I` が 1 に近いところではグラフは直線である、ということだ。 `N/rho` が 4 に近いところの前後のデータをとって線形補間すればよい。 わざわざニュートン・ラフソン法を使う必要性はないと思われる。
表 モデルの補間数値例
このように補間で求めてみると、`zeta_1 / (zeta_1+zeta_2) lt 0.3536` の結果が得られる。 よって、`N/rho` が 1 に近い場合では、線形補間でも問題がないと思われる。逆に、 `N/rho` が 0 に近い場合でもグラフの形状から線形補間は可能である。
さて、カーマックとマッケンドリックの近似式や、ケンドールの解析などを扱ってきたので、 最後にこれらの比較をしよう。
流行が弱いときとは、流行の強さ I が小さいとき、と解釈できる。
例えば、N = 105, ρ = 100 とする。このとき `N/rho` = 1.05 である。
(K8) を`N/rho`が与えられた時の I に関する方程式とすれば、I = 0.0937 が数値計算で得られる。
この数値計算であるが、ニュートン法を用いて近似をすればよい。このとき適用すべき式は、
`f(x) = -log(1-x)/x`
`f'(x)= log(1-x)/x^2 + 1/(x(1-x))`
である。
ニュートン法については、ゴールシークのページを参照してほしい。
さて、今までの結果を下記の表にまとめた。実質的には本書の p.208 表 4 と同じである。 ただし、流行の強さ I に関してのみ、私が検算した結果を表示している。特に、 閾値が 1,000 の場合の本書表4 では流行の強さは小数点第３位までしか表示していないが、 下記の表では、小数点第４位まで表示している（本書表４の閾値が 100 の場合と同様にした）。 閾値、住民総数、比、流行の強さについては今までに述べたとおりだ。 K.M. とあるのは、カーマックとマッケンドリックによるモデルを意味している。 粗近似、精近似ということばはここだけの造語で、 前者は本書でいう、あらい近似式による結果 A2 を指し、 後者はよりよい近似式 A3 を指している。
これだけ数式やグラフを出して、一体何がいいたいのかといえば、
感染症のモデルは難しい、ということである。それでは何も言っていないではないか、
とさらに問われると、せいぜい
今起こっている感染症に関しては、人が多いところにはなるべく出かけないようにしよう、
ということを答えるしかない。これは微分方程式のうちの一つ、
`(dy)/(dt)=betaxy - gammay`
の `beta xy` の項を減らすことにつながるからだ（2020-02-29）。
数式表現には MathJax を使っている。
