サッカー競技場で数学しよう

 
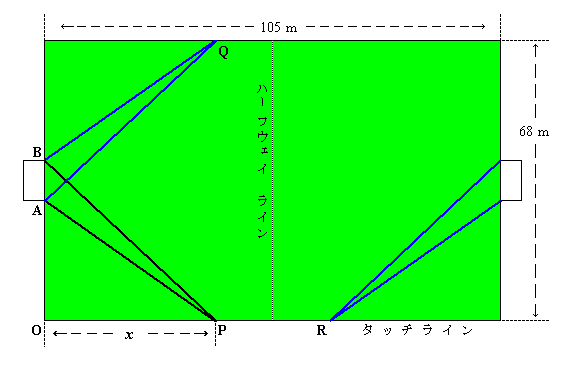
サッカー競技場でタッチライン上から，ゴールの両端を見渡します．

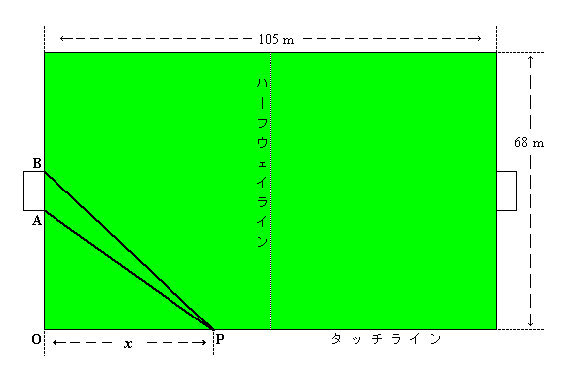
コーナーの位置Oから見るとゴールの両端は重なってしまい，視角は0°です．
ハーフウェイラインの方向に移動していくと，視角は大きくなっていきます．
しかし，ゴールまでの距離が遠くなるので，ある位置を過ぎると視角はまた
小さくなっていきます．

では，
            タッチライン上でゴールの両端を見渡す視角がもっとも
            大きくなる地点はどこでしょうか？

図のように OP =ｘ として，ｘの長さを求めてください．
他の長さは次の通りとします．

  • コーナーから手前のゴールポスト(内側)まで： OA = a = 30.34m
  • ゴール(内側)の横幅：                       AB = b =  7.32m
    • また，角は ∠OPA＝α,∠APB＝β と表すことにします．
    フィールドは長方形ですから，∠AOP は直角です．

    問題を言い換えると

                βが最大となるときのｘの値を求めてください

    ということです．

    【解法 その１】高校生，大学受験生の方法

    高校数学の問題として一般的に解いてから，a,bの値を代入します．

    解法に必要な定理は

    で，受験問題としては基本的な難易度です．0.01m単位まで求めてください．

    実は，オリジナルは信州大学（理・医）2003年度入試問題で，
    これをサッカー場の数値を当てはめて改作したものです．
     

    【解法 その２】現代ビジネスパーソンの方法

    Excelなどの表計算ソフトを使って，シミュレーションします．
    この"シミュレーション"はサッカーのファウルではなく，もともとの意味です！

    最初は粗く，次に範囲を絞って細かく行うとよいでしょう．
    「ソルバーで一発解決」などという手法が使える方はそうしてください．

    必要な計算式，関数は

  • tanの値から角（ラジアン）の値を求める関数 （ Excelでは ATAN ）
  • ラジアンと角度の変換式 （ラジアンのまま計算をしてもかまいません）
    • です．0.1m単位まで求めてください．

    解答例の Excelファイルは下記からダウンロードできます．

    Excel 97以降で動作可．約140KB．
    マクロを使用していますので，ファイルを開く
    ときに警告メッセージが出ることがあります．

    fbfield.xls
    【解法 その３】 Cabriのような幾何ソフトがあれば，これを使うほうが最適でしょう．
     
    YOSHIDA Hajime 2003
    ※１．佐藤勝彦さんから Cabri による解答をいただきました．下記の佐藤さんのページをご覧ください．(2003.12.30)
    http://www.ocv.ne.jp/~ksato/Tezukei/Football/Football.html   （Javaを有効にしてください）
    ※２．松崎康弘さん（サッカー審判員）から下記のようなご教示をいただきました．（2004.1.3）
    実際のサッカー競技では，２人の副審はそれぞれ主に担当するゴールサイドがあるので，問題とは逆の位置の Q,R から青色の線のようにゴールを見ることが多いのだそうです．数学的には上下・左右共に対称ですので，問題の通りの解を他の３つの位置にも適応できます．