◎電界(電場): 電荷(帯電体が帯びている電気のこと)に静電気力を及ぼす空間を電界,もしくは電場と言います。
◎電界の方向と大きさ: 単位正電荷(+1Cの電荷)が受ける静電気力の方向・大きさをもって定義します。
したがって,電気量 $q$ の電荷が電界 $\Vec{E}$ の電界中で受ける静電気力 $\Vec{F}$ は,\[\Vec{F} = q \, \Vec{E} \]で与えられます。$q > 0$ なら $\Vec{F}$ は $\Vec{E}$ と同じ向きですが, $q < 0$ の場合は $\Vec{F}$ は $\Vec{E}$ と逆向きになります。また大きさ $ |\Vec{F}|$ は,\[|\Vec{F}| = |q| \times |\Vec{E}| \]となります。
複数の電荷による合成電界 $\Vec{E}$ は,それぞれの電荷がつくる電界のベクトル合成となります。\[\Vec{E} = \Vec{E_1} + \Vec{E_2} + \Vec{E_3} + \cdots\cdots \] ◎電位: 単位正電荷(+1Cの電荷)が基準点に対してもつ静電エネルギー(静電的な位置エネルギー)。
したがって,電気量 $q$ の電荷が電位 $V$ の電界中でもつ静電エネルギー $U$ は,\[U = q\, V\]となります。
電位の基準点は任意ですが(つまり,どこでも良い),点電荷の場合は「無限遠」とするのが一般的です。
複数の電荷による合成電界の電位は,それぞれの電荷による電位の和となります。\[V = V_1 + V_2 + V_3 + \cdots\cdots \] ◎点電荷がつくる電界: 電気量 $Q$ の点電荷がつくる電界 $\Vec{E}$ は, $Q > 0$ なら点電荷から遠ざかる向きに, $Q < 0$ なら点電荷に近づく向きで,点電荷から距離 $r$ の位置における電界 $\Vec{E}$ の大きさ $|\Vec{E}|$ ( $E$ とも記す) および電位 $V$ は,電位の基準点を無限遠として,\[|\Vec{E}| = k\,\bun{|\,Q\,|}{r^2} \cdots\cdots\maru{1} \\ V = k\,\bun{\,Q\,}{r} \]で与えられます。ここで $k$ はクーロンの法則に関する比例定数で,\[k = \bun{1}{4\,\pi\,\varepsilon_0}\] であり, $\varepsilon_0$ は真空の誘電率と呼ばれる物理量です。
◎電気力線: 電界の様子を視覚的にとらえるために導入された概念で,電界方向を接線にもつ曲線または直線で,正電荷から出て(もしくは無限遠からやってきて),負電荷または無限遠に向かう,と約束します。
◎ガウスの法則: 電界の強さが $E$ のところでは,単位面積当たり $E$ 本の電気力線が貫いていると約束します。
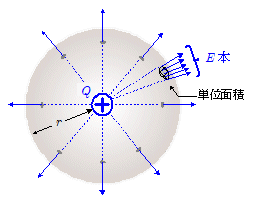
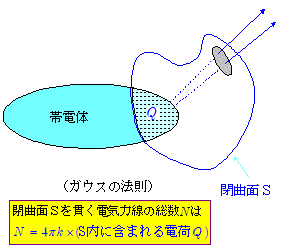
上図のように,正の点電荷 $Q\,(\,>\,0\,)$ を中心に半径 $r$ の球面を考えると,点電荷 $Q$ から出た電気力線はすべてこの球面を貫くので,点電荷 $Q$ から出た電気力線の総数 $N$ は,この球面を貫く電気力線の総数に等しくなります。球面上での電界の強さを $E$ とすれば,単位面積当たり $E$ 本の電気力線が貫き,また点電荷がつくる電界の大きさ $E$ は先の $\maru{1}$ 式で与えられるので,\[N = E\, \times \, 球の表面積 \\ \quad = k\,\bun{\,Q\,}{r^2} \times 4\pi\,r^2 \\ \quad = 4\pi\,k\,Q \quad〔\mathrm{本}〕\\ \quad = \bun{Q}{\varepsilon_0} \quad〔\mathrm{本}〕 \] 以上は点電荷と球面との例で述べたものですが,この考え方をさらに一般化したのがガウスの法則です。すなわち,任意の閉曲面を考えたとき,この閉曲面を貫く電気力線数 $N$ は,その閉曲面内に含まれる電気量を $Q$ として, \[\bbold{ N = 4\,\pi\,k \, Q\,\,〔\mathrm{本}〕\ = \bun{Q}{\varepsilon_0}\,\,〔\mathrm{本}〕} \] で与えられる……というものです。
◎等電位線: 電位の等しい点を結んだ線(3次元空間であれば等電位面)。等電位線上で電荷を移動させても,静電エネルギーは変わりません。
◎電界の強さと等電位線の関係: 等電位線は,重力場における地図の等高線に相当するものです。一方電気力線は,山の斜面に沿って高所から低い方へと水が流れるときの水の流路・道筋に相当するものです。
斜面の勾配が大きいほど水は勢いよく流れるのと同様に,電界の強さは電位が急激に変化している所ほど強くなっています。つまり,電界の強さは電位の距離勾配に比例します。したがって,等電位線の立て込んでいるところほど,電界の強さが大きいことになります。式で表すと,以下のようになります。
電界の方向は電位の減少する向きなので,電界方向にはかった微小距離を $\varDelta r$ として,\[ | \Vec{E} | = -\,\bun{\varDelta V}{\varDelta r} \]
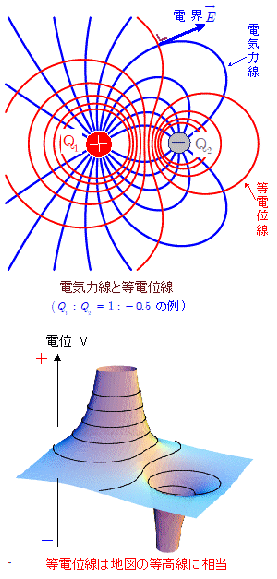
◎電気力線と等電位線の関係: 等電位線に沿って電荷を移動させても静電エネルギーの増減はありません。しかし電荷は電気力線の接線方向(=電界の方向)に電気力を受けているはずです。電気力を受けているのに位置エネルギーが変化しないのは,電気力(=電気力線の接線方向)と,電荷の移動方向すなわち等電位線の方向が直角をなしているからです。つまり,電気力線と等電位線とは互いに直交していることになります。
◎電気力線の特徴: 電気力線どうしは交差しません。なぜなら,もし電気力線が交差するとすればその点において電気力線に対する接線が複数本引けることになり,電界の方向が一方向に定まらないことになるからです。
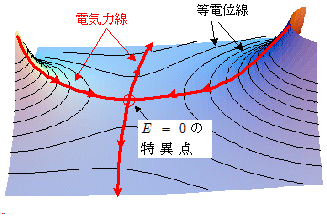
ただし例外的に,電気力線が交差しているような形になる特異点があります。
それは,複数の電荷によってできた電界において,電界の大きさが「0(ゼロ)」になっている点(以下,特異点と表記)です。
この特異点に複数本の電気力線が向かうとき,これらの電気力線は特異点に達した時点で消滅することになるはずです。なぜなら,電界が「0(ゼロ)」ということは,電気力線の定義上,電気力線そのものが存在しないからです。
一方,その特異点のごく々々近傍において,入り込んできた元の電気力線とは異なる方向に電位差が生じていれば,その方向には電界がある,つまり電気力線が存在することになります。
結局,特異点に入り込んできた複数本の電気力線は合体後,1本ないし複数本の電気力線になって新たな向きに続いていく・・・と考えることができます。
消滅したはずのものが再び復活・・・などと何かちょっと苦しい言い訳のようでもありますが(まさに『特異点』の骨頂!),ともかくも特異点においては,電気力線は交差しているように見えることになります。
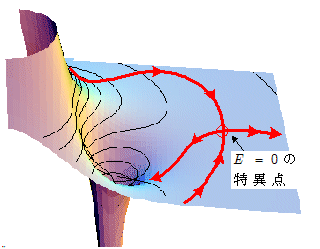
この辺の事情は,馬の背に載せる鞍(くら)の形をした地形(両側が高く,これに直角な両側が低くなっている。下図)に沿って流れる水の流れをイメージすると良いでしょう。図のように,両側の山から流れ出てきた水がぶつかり合って合流し,直ちに二手に分かれて谷側に向かって流れていく……。このような地点での地形の勾配は 0(ゼロ)になっており,これが「電界の大きさが 0(ゼロ)である位置」ということに対応していることになります。