高校では，単振り子の周期
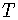は，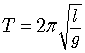
と習います。ここで
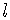は振り子の長さ，
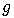は重力加速度です。したがって周期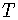は糸の長さだけで決まり，振り子の振幅に関係しません。これはまさに，振り子の等時性を表していますね。しかしこの周期の式は振幅がきわめて小さい場合にしか成立せず，実際には振れ幅の増大とともにその周期
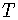も増大していきます。つまり，周期は振幅に依存するわけです。このシミュレーションでは，振り子の運動を，等時性を示す単振動としてシミュレートした場合と，等時性が成り立たない円運動としてシミュレートした場合とが比較できます。
いろいろと振幅を変えてみて下さい。両者の違いがはっきりしてきます。