先入観の影響を受けないで機器の評価をするには、銘柄が何かを教えないで評価するいわゆるブラインド・テストを行なう必要がある。ブラインドテストにも色々なレベルがあり、学問的に認められているのはダブル・ブラインド・テスト(2重盲検法)である。2重の意味は、被験者のみならず施験者も内容を知らないという意味であり、さらに、オーディオ装置の評価などにはABX法がよく採用される。この場合、A、B
,
2つの機器の聴き比べをするわけだがその良否を当てるわけでなく両者の間に差があるかどうかのみに注目する。
今仮に、AというアンプとBというアンプを比較する場合、被験者が Aと感じた場合
a と回答し、Bと感じた場合を b と書くとする。このような試行を一定間隔で何度も繰返すわけであるが、AにするかBするかは無作為(ランダム)でなければならない。つまり、切り替える操作は被験者に知らせるが、A→A、B→B と実際には変わっていない場合も切り替えとみなす。こうすると、AとBが実は同じもの、あるいは実質的に差が無いものだと、正答率が
50% になるはずである。もちろん、試行回数が有限なので50% からずれるが、統計処理を施し、有意差の有無を決める。このとき、被験者の回答がAとBとを完全に取り違えて回答した場合も、変化の有無を正しく検知しておれば有意差ありと認定する。つまり、A→Bと替えた時の回答がb→a、或いはA→A
と替えた時の回答が b→b であっても正しく差の有無を検知したと見做す。最初のボタンの掛け違いは無視し、AかBのどちらかを当てるのではなく、AとBに差があるかどうかのみに注目するわけである。
その統計的評価であるが、正答率が50% となる試行としてわかりやすいのは硬貨投げである。今、硬貨投げを4回行なった場合を考える。当然、2回が表、2回が裏と出る確率が高い(4C2/16=0.375)わけであるが、4回とも表になる確率も 1/16=0.0623 となり、あり得ないわけではない。つまり、
4回とも表が出たからと言って硬貨に仕掛けのあるインチキ賭博であると断定することは出来ない。では、8回投げた時はどうだろうか。全てが表になる確率は、1/16/16=0.004 で、8回投げるという試行を256回繰返して1度起こるという稀な現象であり、のっけから、8回全て表が出れば、誰しも硬貨に何か仕掛けがあることを疑うであろう。つまり、表と裏が出る確率に有意差があると考えるわけである。その境界を決めるのは難しいが、普通、確率が
0.1以下になるような結果が出れば、表と裏が出る確率が等しくない原因があると疑うのではなかろうか?
ABXテストの場合、統計評価は普通 X2 (カイ二乗)検定法がで行なう。実際の適用法は後述。
施験者もA,B どちらを使っているのか分からないようにしてテストを行なうのはなかなか難しい。パソコンで乱数を発生し、奇数ならA、偶数ならB に繋がるようスイッチ・ボックスをコントロールし、その順序を記録しておき、後で回答と比較し統計処理を施す、といった装置が出来れば理想的である。この場合は施験者が機械であるため、1人で気が済むまでテストできるので信頼できるデータが得られる。外国にはこのような操作をやってくれる装置が市販されているそうである。人に手伝ってもらうときは、スイッチ・ボックス共々他室でやるか、衝立の陰で切り替えを行なう必要がある。この場合、音で切り替えの有無が分からないように、中立端子付きの3接点のスイッチを使い、一旦中立に戻した後A,Bどちらかに切り替えるのがよいだろう。どちらに切り替えるかもその時の気まぐれでなく、乱数表を用意しておき、スタート時に適当な所から奇遇に応じA,B を切り替えるといいだろう。
切り替えの方法は機器の種類により異なるだろうし、最適の方法を工夫する必要があり、最も難しい点である。
簡単のため、A、Bどちらの機器を使ったかを10回の試行を行い当てる場合を例にとり説明する。実際には少なくとも16回以上行なう必要があるといわれている。親ページにリンクした測定例では、数十回から、百回以上の試行でテストしておりかなり信頼できるテストである。
| 順番 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 試行回数 n=10 | |||
| 乱数 | 3 | 6 | 9 | 6 | 4 | 4 | 3 | 6 | 6 | 1 | ||||
| A/B | A | B | A | B | B | B | A | B | B | A | ||||
| 回答 | b | b | a | b | b | a | a | a | a | a | 正答回数 m | X2 | p | 判定 |
| 正誤 | × | ○ | ○ | ○ | ○ | × | ○ | × | × | ○ | 6 | 0.4 | 0.53 | 有意差無 |
(a) 有意差の無い場合の例
被験者は空色の部分だけの表をもらい、回答欄にその順番の機器をAと感じたかBと感じたか書き込む。
この例では回答欄も乱数表の別の場所の並びから奇数 a、偶数 b として書き入れてある。乱数表はエクセルのRAND
関数を使って作ることが出来る。
| 順番 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 試行回数 n=10 | |||
| 乱数 | 3 | 6 | 9 | 6 | 4 | 4 | 3 | 6 | 6 | 1 | ||||
| A/B | A | B | A | B | B | B | A | B | B | A | ||||
| 回答 | a | b | a | b | b | a | a | b | b | a | 正答回数 m | X2 | p | 判定 |
| 正誤 | ○ | ○ | ○ | ○ | ○ | × | ○ | ○ | ○ | ○ | 9 | 6.4 | 0.011 | 有意差有 |
(b)有意差のある場合の例
上表の1、8、9番を正解とした。被験者が少なくとも1、8,9番目は正しく違いを感じている場合に相当する。
ABX法のように2者択一のテストは自由度1のカイ二乗分布に従うとしてよく、X2 は下式で与えられる。
X2={4×(m - n/2)2}/n (1) (n:試行回数、 m:正答数)
これに対する、確率 p は X2 分布表から求めることが出来る。あるいは、エクセルの統計関数を使って求めることも出来る。関数名は
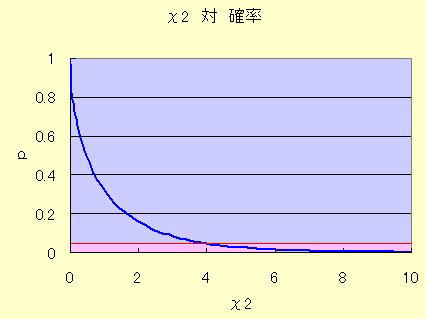
CHIDIST である。下に、X2 と確率の関係をグラフで示す。
例示した表に(1)式で求めた X2 の値と、それに対し下図から読み取った、p の値を示す。
X2 の大きさは、A、Bに差が無い場合の平均正答数(この場合5)からのずれの大きさを表し、p はこのずれが統計的ばらつきで起こる確率を示す。
本当に差が無い場合は、当然 X2 の値は小さく、確率 p は大きい。この場合、有意差無しと判定する。
逆に、実際にはA,B 間に誰が聴いても差がある物であれば、正答率は高く、X2 値は大きくなり、p は小さくなる。pの値がある境界値(0.05 くらい)より小さい場合は有意差有と判定する。その理由は、A,B に差が無い場合にこのような結果(X2 が大きい)が出る確率は極めて小さいので、差が無いという仮定が誤りで、有意差有と解釈するわけである。
例(b)の場合、pが0.011と小さく有意差有と判定する。10個のコイン投げで9回も表が出た場合、コインに何か仕掛けがあるはずだと疑うことに相当する。
もし、正答が8回であれば、p=0.06 となり、判定は微妙になる。このような場合は、試行数を増やして(例えば50回)再度行なう必要がある。そうすると、差が無い場合はpは大きい方に、差がある場合は小さい方に偏って行き、より確かな判定が出来るはずである。
また、(1)式を見れば分かるが、○と×が全く逆の答であっても、X2値、p値 は変わらず、このテストがAかBを当てるテストでなく、差があるかどうかのみを調べるテストであることが分かる。

自由度1のX2 分布にたいする、X2 値と確率 p の関係。
下のピンク色の領域は有意差有りと判定する領域。ただし、境界付近の値が出た場合は判定は微妙で、試行回数を増やして確かめる必要がある。