|
高橋至時『ラランデ暦書管見』と光行差 上 原 貞 治 1.はじめに 志筑忠雄は、ジョン・ケイルの書いた物理学・天文学の手引書(ラテン語原著のオランダ語版)を翻案し、日本語の書物『暦象新書』にして紹介した。彼は、ニュートン力学をほぼ完全に理解し、ケプラーの法則の証明や楕円運動の計算法を誤りなく訳出することができた。彼は日本初の物理学者と言えるレベルまで達したが、職業的な天文学者ではなかった。
そして、本職の天文学者で初めて専門的な西洋書を研究し、その近代科学の精神に触れたのは幕府天文方の高橋至時であった。彼が手引きとして利用したのは、ケイルの書よりも新しい『ラランデ暦書』(フランス語原本のオランダ語訳。原著Jerome de Lalande著"Astronomie"
(1764)、オランダ語訳A.B. Strabbe訳"Astronomia
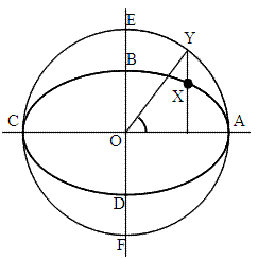
of Sterrekunde")であった。本稿では、高橋至時が『ラランデ暦書』を読んで書いた『ラランデ暦書管見』の光行差に関する部分を検討し、彼の解読と研究の状況を議論する。実は、彼は光行差の理由を理解することがまったくできなかった。 当時の日本最高の専門家の頭脳を持ってしても到達できなかった西洋天文学、物理学の概念を探ることは、高橋至時の偉業の最前線をたどるとともに、文化の異なる土壌における西洋近代科学の理解を論ずる点でも興味深いことであろう。 これは、極めて含蓄の深い、学問上の問題提起の幅の広い現象である。恒星の位置観測において補正が必要になるということを別にしても、天文学における第一級の重要事項に属すると言ってよいであろう。それは、ブラッドリー(James Bradley, 1693 -1762、英国)による発見(1728)以降19世紀までの天文学において、次のような意義を持っていた。 ・地球が太陽の周りを公転していることの証明 実際、地球の公転運動が物理的に確認されたのは光行差の発見が最初である。また、当時、すでに光の速度の有限性は、レーマーによる木星の衛星の周期の変化の観測によって判明していたが、光行差の観測によってその精度は向上した。さらに、その後、光行差が、地球、恒星、宇宙空間の三者の相互関係に依存するという考察から、光を伝える媒質(エーテル)の存在についての議論・実験を経て、ついに20世紀には相対性理論の基礎となる光速度不変の原理にたどり着く。現代の物理学では、光行差は本質的に特殊相対性理論のローレンツ変換の計算に帰着する。 高橋至時は、光行差が生じる理由を理解できなかったので、このような意義については思いを馳せることすらできなかった。 文献[1]の抜粋は編者の中山茂氏によって行われているが、これは氏が特別にこの部分を偏重しているわけではない(重要性を高く認めておられていることは間違いないが)。原資料(筆者が参照するのは、羽間文庫・間五郎兵衛蔵書本[2])で、72丁(144ページ)ある『ラランデ暦書管見』第八冊のすべてが光行差に関する記述なのである。なぜ高橋は理解できない光行差をここまで掘り下げて議論したのだろうか。いきなり的外れな推測をしてもよくないので、これについては最後に議論することにしよう。 以下は、『ラランデ暦書管見』第八冊(以下、「管見」と略す)の粗々の構成である。ここでは、上に挙げた本[2]に依った。 第八冊は、「恒星五星アベルラテイ」変差之巻」(閉鈎括弧はママ)と題されている。「アベルラテイ」とは光行差(aberratie、オランダ語。発音は「アベラティ」に近い)のことであるが、高橋は、音訳で記述している(元来は、「ずれ」とか「偏差」程度の意味である)。高橋は、巻の冒頭で、アベルラテイと「ニユタテイ」(これは光行差の精密測定の過程で発見された「章動」のことであるが第八冊に具体的な議論はない)を紹介し、これらがロンデンに住むブラトレイという人(地名、人名はママ)によって1728年に確立されたことに触れている。その発見の経緯については、「ゴロート・セキトル(Grooten Sector)」と呼ばれる「遠鏡儀」が使われたということのみが書かれている。 「管見」は、アベルラテイの現象の概略と詳細を図を使って説明している。しかし、現象の理由については理解できないとする。そして、光行差が恒星と太陽の黄経差と黄緯の関数として数式として表現できることと、アベルラテイの大きさを現す角度の量20"(光行差による楕円運動の半長径。単位は角度の秒で1度の3600分の1)が、地球が太陽の周りを8分間に公転する角度であることが述べられる。そして、具体的な恒星を例に取って、アベルラテイの動きが取り上げられ、数値を用いた計算がなされる。高橋は、すでに、惑星の運動を地動説で計算できたので、この種の計算にはまったく違和感がなかったものと思われる。 そのあと、アベルラテイの動きが黄道座標から赤道座標に変換され、赤緯のずれの最大値とその日時が議論される。これは三角関数を用いた相当に複雑な計算だが、高橋はフォローしているようである。しかし、複雑といっても、これは球面幾何の問題で、観測データの解析以上の深い天文学的意味があるものではない。そして、惑星におけるアベルラテイの計算方法(惑星は自身の運動が問題になるので計算の方法論が少し違う)に言及して巻を終える。『ラランデ暦書管見』の完成稿本は全八冊であるので、これで全編の終わりとなる。 なお、巻のあちこちでアベルラテイが視差(正確には年周視差)と比較される。恒星の視差の原理について高橋は完全に理解していた。年周視差は、いわば惑星が順行・逆行を繰り返すのと同等の現象である。地球の公転運動の証拠となるこの効果は長らく予想されていたが、当時の西洋でもまだ検出されていなかった。ブラッドリーの光行差の発見観測もそもそもは視差の検出を動機としたものであり、光行差の発見は予期されていなかった。高橋は、視差と光行差が位相角(*1)で90度ずれていることを指摘し、その理由がわからないとしている。また、光行差を視差に類似した効果として理解することを試みたものの、その大きさが星までの距離に依らないこと(彼は恒星ごとにその距離が違うことを知っていた)をまったくの不思議としている。また、アベルラテイの観測誤差がこの疑問を生ませているのではないかと疑っている。 (*1)楕円上の点の位相角については、本稿の終わりに補足として図解する。
高橋が「管見」第八冊を書くのに使ったのは、蘭語本第3巻(1777)の第17部である。そこでは、もっぱら光行差aberratieと章動nutatieについて書かれている。その§2790〜2852が、高橋が読んだ光行差についての記述である。 始めのほうに、ブラッドリーによる発見の経緯と現象の概略および観測の過程が書かれている。そして、光行差による恒星の動きの計算法、計算例、視差との関連、赤道座標系での動き、があり、最後に惑星の光行差の記述となっている。高橋の「管見」が、大筋でそれを順にフォローしたことを示している。「管見」には蘭語本のページ数や章番号、図番号が書かれているので、両者の対応を取ることはたやすい。 さて、内容の比較である。高橋至時は、ブラッドリーが光行差を発見した経緯を紹介していない。文章が理解できなかったようである。光行差の原因となる光速の有限性については、まったく考えが及んでいないが、結論から言うと、彼はオランダ語の「速度」という単語が理解できなかったようである。ちょっと突飛な想像かもしれないが、もっぱら天体の見かけの動きを扱っていた当時の日本の天文学者は、速度の概念にほとんどなじみがなかったために、単語集に拾われなかったのかもしれない。ちなみに、志筑忠雄は、ニュートン力学の解説で、速度のことを「速力」と呼んでいる。これは、西洋語の訳語で、志筑の造語だと言われている。 驚いたことに、高橋は、光行差の現象の詳細については非常に正確に把握している。もちろん、この蘭語本を読んで理解したのである。彼は、オランダ語の知識は不十分でも計算の部分はほぼ完全に理解した。光行差によって恒星が楕円周上を地球が進行する方向に寄るように動くこと、その長軸が黄道に平行になり、半長径は20"で、黄緯方向(半短径)はそれに黄緯の正弦をかけた量になること、そして星が楕円上を回る方向が黄緯の正負によって変わることなど、すべて完璧に把握している。また、蘭語本に、1箇所、正弦(sin)と余弦(cos)の間違いがあるが、高橋はこの間違いを指摘している[1]。彼は計算を理解することによって読み進んでいるのである。 原著者ラランドは読者がテキストの理解から計算の理解へと進むことを想定してこの本を書いたが、高橋はこれを逆に計算の理解からテキストの解釈へとたどった。それはおおむね成功しているが、一部でその弊害のため、高橋は観測や計算の事実と根拠の論理を取り違えたような解釈をした。その具体的な点について次節で紹介する。
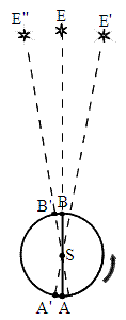
6.1 光行差の発見とその解釈 光行差は、ブラッドリーの観測によって、天頂付近を通過する特定の恒星の見かけの赤道座標(赤緯)が公転軌道上の地球の位置(すなわち季節)ごとに変わることから発見された。彼は、その動きがどの恒星でも長径40"の楕円になっていることを突き止め、最初はその理由を不審に思った。蘭語本はこの発見経緯と観測を述べて、§2798に次のように書いている。(筆者訳。ここで、括弧内は筆者による補足) ブラッドリーは、偶然、この40"の差が、ちょうど地球が16分間に動く公転軌道上の角度であることに気づいた。レーマーが1675年に成し遂げた発見によると、光は、この16分で地球の軌道の直径を突き進む。ブラッドリーは、(自身の観測結果を)まず次のように表現した。星が「合」(太陽と同じ黄経)の位置にある時から「衝」(太陽との黄経差が180°)の位置に来るまでの時間が16分だけ長く見え、「合」の時に恒星の黄経が40"だけ少ない(西に寄った)ように見える。 後半の表現については図1を参照されたい。そして、ブラッドリーは、次のような原理の計算をして光行差の観測を光速と結びつけた。上で彼が気づいた事実は、 360°:40"=1恒星年:16分、 および (1) 地球軌道の直径:地球が16分間に進む距離=c:v、 (2) ということである。ここで、cは光速、vは地球の公転速度である。これらの式を用いて、光速と地球の速度の比を、地球軌道の半径を単位とした進行距離の比で表すと、 c:v=2:(40"/3600/180)π (3)(角度の単位を、"からラジアンに換算した) という関係が導き出される。これは「雨傘理論」(速度ベクトルの合成)によって、地球の進行方向に対して直角の方向にある恒星を見た場合(本稿の図2参照)の予想である c:v = 1:tan θ (4) と一致する。ここで、θ=20"である(微小角については、ラジアン単位のθ≒tanθが成り立つ)。これで、光行差の観測と雨傘理論の関係が確立した。 いっぽう、高橋至時は、観測の経緯の部分とレーマーが最初に測定した光速との関連の部分は見逃してしまい、(または、気づいたかもしれないが、その意味は読み取れずに)ブラッドリーが現象の説明のために仮想した部分を発見観測そのものと誤解した。以下は「管見」からの抜粋である(「管見」の抜粋は、仮名や漢字を適当に置き換え、送り仮名、句読点などを補った。括弧内は原文では二行割註) 又二千七百九十八章に云ふ所を見れば、これ星と地と同度(夜半に星南中すること也)より相隔たる半周(これ星と太陽と同度の時也。如何にして測り得しや)の時に至るの日時分を測るに、恒星歳実の折半と差ふこと、時の一十六分なることを測り得て、これよりこの法を巧み出したると見ゆ(時の一十六分中に地の行四十秒也。これ「アベルラテイ」の差の倍数也) 高橋は、どうして太陽と「合」の時に観測が出来たのかと不審に思いながらも、この「16分」のずれをブラッドリーの発見の観測値そのものとしてしまった。そして、光速の関連の部分をすっとばして、16分と40"の関係を単なる地球の公転速度による換算として中途半端なところで納得してしまったらしい。
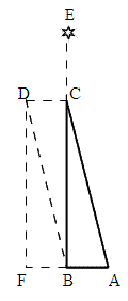
高橋至時は、上記の少し後の部分に次のように書いている。 又二千八百〇六章に一万〇三百一十三倍と云へるは、即ち右の二十秒の余割線也。これ二百三十三図のABとCBとの比例数也。 「二百三十三図」は次節に載せる。これに対応する部分を蘭語本の§2806に捜すと、そこにはつぎのように書かれている(括弧内は概略の意訳)。 (光行差の観測値20"に対応する地球の移動時間を用いると、地球と太陽との平均距離を進む光の所要時間8分7秒に相当することから)光の速度が地球の平均速度より10313倍速いことが導かれる。 この部分は、ブラッドリーの光行差の測定値20"をもとに、上記の式の考察に基づいて、c:v、つまり「光速」を計算で導き出しているところにほかならない。高橋が書いたような単にcot 20"=10313の関係を示しているのではない(*2)。上に見るように、蘭語本には明瞭に「光の速度」、オランダ語で"de snelheid van het licht" と書かれている。つまり、高橋はこのオランダ語が訳せなかったということである。次に見るように、星からの光について彼はいちおう触れているので、単純に考えれば、彼の単語集に"snelheid"(速度)が載っていなかったのが直接の原因であったと考えるほかはない。 (*2) この「8分7秒」は計算値である(365.25日×20"/3600/360=8分7秒)。また、「余割」は三角関数のcosec(コセカント、sinの逆数)であるが、参照している図233によると、ここで高橋はcot(コタンジェント、tanの逆数)を意味しているらしい。角度が微小の時、sinとtanは近似的に一致するので、その違いを問題にしなかったのであろう。 ラランデ暦書蘭語本の図233と図237は、光の速度と地球の公転運動の速度のベクトルを合成して(実際にはベクトルの差をとる)光行差の効果を示している。ここでは、恒星が地球の進行方向に対して直角の方向にある図233を取ろう。図2にそれを示す(*3)。蘭語本§2801には次のような説明がある(筆者訳)。 Eをある星としよう。そこから我々の方向へ光線がやってくる。そして、1つの光の断片がEからBへ行くと見なされる。ABを地球の軌道上の動きの小さな部分としよう。たとえば、それを20"の部分とする(読者は、なぜ我々が20"という数値を選んだかをただちに理解せねばならぬ)。そして、CBは、地球が軌道の一部分ABを動く時間に、光が進む距離である。つまり、光の断片Bは、地球がAにあった時にはCにあった。そして、地球がBに来た時、光もそこに来る。この考え方によって、光と地球の速度が、20"に対応する時間における移動距離CBとABによって導き出される。 高橋至時のこの図の解釈は、少し興味深い。「管見」では次のようになっている(括弧内は二行割註。<>内は筆者の補足)、 △又二千八百〇一章の意は、空中の気へ星光うつ<り>て、地より視てこの差を生じるものと云ふ意と見ゆ。恒星天は至高にして地天の半径すら妨げを為さず。故にこの説を創めしと見ゆ。 ここで「地天」とは地球の公転軌道のことである。蘭語本と比較して、だいたい正しく理解しているように見えるが、実は大きな違いがある。CBを光が有限の時間に進む距離として理解できず、Cに星の光が反映して見えると解釈している。しかし、Cが宇宙空間のどこにあたるのか、地球の動きABが20"だとして、なぜ恒星の位置も同じだけずれるのか、まったく説明がなく解釈ができていないことを示している。 また、高橋がここで「気」というふだん天体観測に乗ってこないものに言及しているのは極めて珍しい。18世紀の西洋の天文学分野では、まだ光波の媒体としての「エーテル」の存在の必要性が確立されていなかったので、これはエーテルではなく、東洋自然哲学の「気」(宇宙にあるすべて物質の根源となる気体状の物質が宇宙空間に希薄に詰まっているとする)を想定した可能性が高い。高橋が苦し紛れに持ち出した説明と言えそうである。 (*3) 光に対し三角形を使って速度の合成をすることは、相対性理論の光速度不変の原理と矛盾しているが、光行差を求めるためのv/cの一次の近似計算としては問題ない。
さらに進んで、高橋は視差と光行差が同時に起こった場合にどのように見えるか、という部分について論考している。彼がこのような込み入った問題まで立ち入っているのは注目に値する。「管見」では以下のように書かれている(括弧内は人名・地名のルビ、または二行割註)。 △二千八百二十七章 蘭語本の§2827には、確かにそのような内容が書かれている。Boscovichは、1742年にローマの大学で出版した論文で、視差と光行差の動きを合成すると、光行差の楕円運動と相似形の楕円が描かれることを示した。蘭語本にはその数学的な証明は与えられていない。ここで、星の位置の位相角は、一定の角度だけずれる。その角度の正切(=正接、tan)は、視差の角度量(星までの距離に反比例するが、当時は未検出)を光行差の角度量(20")で割った値になる。 蘭語本のこの部分の説明は十分でなく、具体的な計算もないので内容を理解するのは困難だっただろうと推測されるが、「管見」の内容はおおむね正しい。「同象」というのを高橋が正しく理解したかはわからないが、これは「相似」という意味である。「正切」のもとになる角度についても高橋は正しく、それは、光行差のみを考慮した場合と視差をも考慮した場合の楕円周上の星の位相角(図3)の差を指している。高橋が、数式がなくても天体の位置に関する幾何についてほぼ正しく読み取ったのは、長年の研究と鍛錬の成果として驚くほかはない。なお、Boscovichの言明は正しいので、蘭語本でそれが否定されているということはない(§2828の内容はBoscovichの説とは関係がない)。 7.志筑忠雄の先行研究 ブラッドリーの業績を日本語にしたのは、高橋至時が最初ではない。それはすでに、志筑忠雄著『暦象新書』中編(1800)に紹介されている。その下巻の「光明有体」の内容は、志筑の考えを述べたもので原書の単なる翻訳ではないが、そこに以下のような記述がある[4](仮名、漢字など読みやすいように適当に置き換えた。括弧内は二行割註)。 ルロフス曰、さきに光明速力のことについて、数件難題ありしかども、皆能く解て、いよいよ光明の速力あるに決しぬと云へり。但し速力有りと云ふは、速力に関係するをいへり。
ロトムルと云ふ者、光明速力の数を測算して曰、光明太陽より地球に至るに、六十分時の十一を以てすと云へり、(即ち我七十六分三十八秒。) ルロフス曰、ブラツトレイの説に依れば、光明速力、ロトムルの言へるよりも甚大なり。然ども又曰、若一箇の恒星、たとえば忽として消えることありとも、月を越て猶能く其の星の天上にあるを見んと云へり。
是等の言を以て観れば、光明の速力あること、また信ずるに足れり。固より既に引力に関わるものなれば、其の速力あるもまた理の当然なり。唯、其の神速譬ふるに物なきのみ。 「ルロフス」は志筑忠雄が用いたオランダ語訳本の訳者、「ロトムル」はレーマーのことである。ここで志筑は、ブラッドリーをレーマーと並ぶ光速度の測定者として扱っている。志筑は光行差については触れていないが、光速が有限であることを、自身の考察も交えて議論している(*4)。ここで、彼が興味があったのは、光の正体とその物理的性質についてであり、恒星の位置が少しずれるということではなかった。志筑は、ニュートンの光の粒子説を連想して、光速度が有限であることを理解し、それを光に働く「引力」の存在と結びつけている。この「引力」は水面などで起こる光の屈折が分子間力のような力の効果によると理解したものである。志筑は、光は「物体」の一種である、ということを主張する根拠として、光速度の有限性を参照したのである。 高橋至時が『暦象新書』を読んでいたなら、ブラッドリーが光速の測定と関係していることを知り、それを光行差と結びつけようとしただろうから、彼が暦象新書を読んでいなかったことがこれでわかる[5]。 (*4) 志筑の引用にあるように、ルロフスはケイルの書のオランダ語訳に、脚注としてブラッドリーの光行差に関する業績を書き加えた[6]。したがって、文献[1]の「アベルラテイ」の註に「カイルの著はブラドレーの発見以前であり、光行差は忠雄にもつたわっていなかったようである」とあるのは正確ではない。 8.まとめ 〜なぜ高橋至時は光行差にこだわったか 高橋は、謎の原因による現象をなぜこんなにも深く掘り下げたのであろうか。第一に、いずれは理解できると考えて挑戦したのであろう。彼は、ケプラーの法則による運動の計算を示した難解と言われた『暦象考成後編』(中国書)を読み、それを応用して惑星の運動の計算方法を打ち立てた。また、英国航海暦の数値を参照する計算もした。計算の実力によって難解な参考書も読解できる自信があったのだろう。彼はラランデ暦書が一筋縄ではいかないことはわかったであろうが、何と言ってもそれに利用できた時間が短すぎた。第二に、光行差は、恒星位置の観測精度に関わる現象であったので無視できず、研究途上であってもそれをできるだけまとめようとしたのであろう。ラランデ暦書の研究の無理がたたって高橋は命を縮めたと言われている。光行差への執念が災いしたのかどうかはわからないが、この現象には何か特別に惹かれるものを感じていたのかもしれない。 彼に「光の速度」というオランダ語の語彙を教える者がいなかったことはまことに残念なことであった。しかし、それにも関わらず『ラランデ暦書管見』第八冊は、高橋至時が並外れた天才であるとともに偉大な努力の人であったことを我々に伝えている。 補足:楕円周上の位相角の定義 図3で定義される楕円周上の点の位相角は、光行差および視差の現象において、地球の公転とともにほぼ一定の割合で増加(あるいは減少)し、1恒星年で1周する(減少・増加の方向は星の黄緯がプラスかマイナスかによる)。
謝 辞 「ラランデ暦書管見」第八冊の複製本の複写の便宜をいただきました大阪歴史博物館に感謝いたします。光行差と視差の合成について数学上の指摘を与えてくれた上原晃人氏に感謝します。
[2] 「西洋人ラランデ暦書管見 八」(高橋至時著(1803)) 羽間文庫・間五郎兵衛蔵書、大阪歴史博物館所蔵、(なにわ歴史塾複製本) [3] 「ラランデ暦書」蘭語本、"Astronomia of Sterrekunde"第3巻 J.
de Lalande著、A.B.Strabbe訳、アムステルダム (1777)(複製版あり、グーグルブックス) [4] 「暦象新書」(志筑忠雄著)(1798-1802)(文明源流叢書第二巻 所載、早稲田大学古典籍総合データべース) [5] 「我が国におけるケプラーの第3法則の受容(II) 麻田剛立 『五星距地之奇法』と志筑忠雄『暦象新書』」の比較」 上原貞治、天界
87, 320-328 (2006), 東亜天文学会 http://www.d1.dion.ne.jp/~ueharas/seiten/rekisho.pdf [6] "Inleidinge tot de waare natuur- en sterrekunde, of de
natuur- en sterrekundige lessen"(原著者J. Keill、訳者J.Lulofs)(1741)(グーグルブックス) |