振動数が $f_1$ の音と振動数が $f_2$ の音が重なったとき,1秒間に聞こえるうなりの回数 $f_\mathrm{B}$ は,\[f_\mathrm{B}=\big|f_1-f_2\big|\] という式でという式で与えられます(導出は後述)。
◎うなりを聴く:
をクリックしてみて下さい。 ( 音量:
)
振動数が $f_1=440\mathrm{Hz}$と$f_1=441\mathrm{Hz}$の音のうなり音が4秒間聞けます。
このときの $f_1$ との $f_2$ との差は1ですから,公式により,このとき聞こえるうなりの回数は,1秒間に 1回 になる筈です。確認してみてください。
ただしうなりは,振動数がわずかに異なる音が重なったときに起きる現象で,振動数が大きく異なるときはうなりとして観測されません。
たとえば,$f_1 = 440\mathrm{Hz}$( ”ラ”の音)の音と $f_2 = 349.23\mathrm{Hz}$( ”ファ”の音)の音を同時に鳴らすと,その合成音はもはやうなりとしてではなく,”ラ”と”ファ”の和音として聞こえます。
をクリック。 ( 音量:
)
◎うなりの数学的な説明・公式の導出
たとえば,次のような2つの波の式で表させる音波が重なったとしよう。\[ y_1=\sin2\pi\bigg(f_1t - \bun{x}{\lambda_1}\bigg) \\ y_2=\sin2\pi\bigg(f_2t - \bun{x}{\lambda_2}\bigg)\] このときこの2つの音波を $x=0$ の点で観測したとすると,それぞれの音波による振動の式は次のようになる。\[y_1=\sin(2\pi f_1 \,t) \\ y_1=\sin( 2 \pi f_2 \,t) \] したがって $x=0$ の点で観測される合成音波の振動 $Y$ は,\[Y=y_1+y_2 \\ \quad =\sin(2\pi f_1\, t) + \sin(2\pi f_2\, t) \\ \quad =2\cos2\pi \bun{f_1-f_2}{2}t\cdot \sin2\pi \bun{f_1+f_2}{2} \,t \] となる。上式が,$2\cos2\pi\bun{f_1-f_2}{2}t$ なる第一因子と,$\sin2\pi\bun{f_1+f_2}{2}t$ なる第二因子との積の形になっていることに注意して下さい。
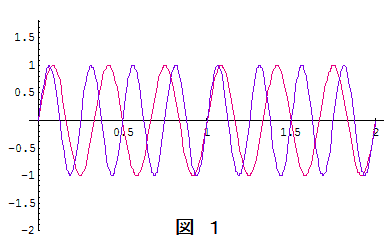
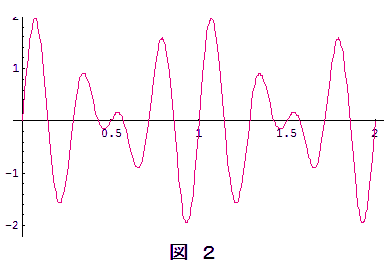
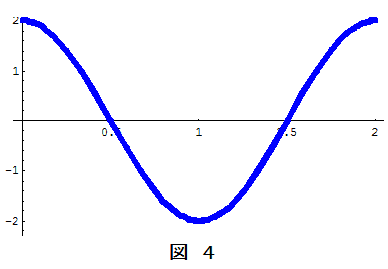
上の図1は $f_1: f_2 = 4:3$ の場合の2つの振動の時間変化で,赤色が $y_1$ を,水色が $y_2$ を表します。その合成振動は図2のようになる。一見複雑な波形に見えますが,これを第一因子 $2\cos 2\pi\bun{f_1-f_2}{2} \, t$ と第二因子子 $\sin 2\pi\bun{f_1+f_2}{2}\, t$ のそれぞれ分けて考えると,第一因子は図4のように,第二因は図3のように時間変化します。実際の合成振動 $Y$ は第一因子と第二因子との積,したがって図3と図4とをかけ算したものであり,図5がその結果です。
このとき第一因子 $2\cos 2\pi\bun{f_1-f_2}{2} \, t$( 図4)はきわめてゆっくりした変化になるため,あたかも第二因子 $\sin 2\pi\bun{f_1+f_2}{2}\, t$(図3)の変化が第一因子で抑え込まれたような形になってしまいます。つまり,第二因子による細かい振動の大きさを第一因子が決定付けていることになり,この第一因子(の絶対値)が合成振動の振幅を与えることになるわけです。
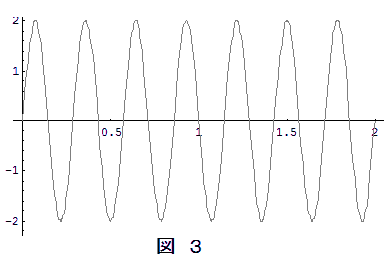
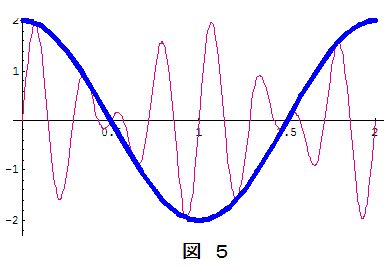
合成振動の振幅が最大になる時間間隔( =うなりの周期)を$T_\mathrm{B}$ とする。ある時刻 $t_0$ に振幅が最大であったとすれば,次に振幅が最大となるのは時間 $T_\mathrm{B}$ 後ゆえ(以下では $f_1>f_2$ と仮定する),時刻 $t_0$と $t_0+T_\mathrm{B}$ に第一因子の絶対値が最大になるとおいて,\[2\bigg| \cos2\pi\bun{f_1-f_2}{2}\,t_0\bigg|=2 \\ \quad\quad\therefore 2\pi\bun{f_1-f_2}{2}\, t_0=m\pi\quad(m:整数)\cdots\cdots\maru{1}\\ 2\bigg| \cos2\pi\bun{f_1-f_2}{2}(t_0+T_\mathrm{B})\bigg|=2 \\ \quad\quad\therefore 2\pi\bun{f_1-f_2}{2}(t_0+T_\mathrm{B})=(m+1)\pi\cdots\cdots\maru{2}\] $\maru{2}-\maru{1}$ より,\[\pi(f_1-f_2)T_\mathrm{B}=\pi\quad\quad\therefore (f_1-f_2)T_\mathrm{B}=1 \\\therefore \color{red}{うなりの振動数 \,f_\mathrm{B}=\bun{1}{T_\mathrm{B}}=f_1-f_2} \] となる。
つぎに,波長が異なる2つの波が重なったときの空間的な周期性について考えよう。
先の波の式 $y_1$ , $y_2$ において,時刻 $t=0$ における波形を考える。前式に $t=0$ を代入して,\[y_1=-\sin\bun{2\pi}{\lambda_1}x \\ y_2=-\sin\bun{2\pi}{\lambda_2} x \\ \kern-2em \therefore Y_{t=0}=y_1+y_2 \\ = -2\cos 2\pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)\bun{x}{2} \cdot \sin 2\pi\bigg(\bun{1}{\lambda_1}+\bun{1}{\lambda_2}\bigg)\bun{x}{2} \] この場合も先の例と同様に第一因子$-2\cos \pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)x$ と第二因子 $\sin \pi\bigg(\bun{1}{\lambda_1}+\bun{1}{\lambda_2}\bigg)x$ とに分けて考えると,$x$ に対して第一因子はゆっくりとした変化を示し,第二因子は細かい変化を示すことになる。したがって全体として,第二因子で示される波形を第一因子が抑えつける効果を持ち,第一因子の絶対値がこの場合の波形の振幅を表すことになる。そこで座標 $x_0$ と隣接して座標 $x_0+L_\mathrm{B}$ において振幅最大になったとすると,\[\bigg|\cos \pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)x_0\bigg|=1 \\ \quad \therefore \pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)x_0=m\pi \\ \bigg|\cos \pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)(x_0+L_\mathrm{B})\bigg|=1 \\\quad\quad \therefore \pi\bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)(x_0+L_\mathrm{B})=(m+1)\pi \\ \quad \therefore \bigg(\bun{1}{\lambda_1}-\bun{1}{\lambda_2}\bigg)L_\mathrm{B}=\bun{L_\mathrm{B}}{\lambda_1}-\bun{L_\mathrm{B}}{\lambda_2}=1 \] ここで$\bun{L_\mathrm{B}}{\lambda_1}$,$\bun{L_\mathrm{B}}{\lambda_2}$ は,波長 $\lambda_1$, $\lambda_2$ の波 $y_1$, $y_2$ が距離 $L_\mathrm{B}$の区間の中にそれぞれ何個分ずつ含まれているか,その個数を表す。このことから,波長の異なる波が重なったとき,空間的には,
波の個数の差=1
となるごとに振幅最大の箇所が出来ていることになる。
戻る