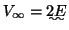図のように電池
![\includegraphics [scale=1.2]{C1-1.eps}](img10.gif)
- (1)
- まずスイッチ
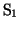 ,
,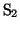 を同時にA側に接続した。このときコンデンサー
を同時にA側に接続した。このときコンデンサー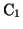 の両極板には
の両極板には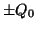 の電荷(電気量)がたくわえられた。
の電荷(電気量)がたくわえられた。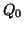 を求めよ。
を求めよ。

- (2)
- その後スイッチ
 ,
, を同時に切りかえてB側に接続した。このとき,コンデンサー
を同時に切りかえてB側に接続した。このとき,コンデンサー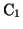 ,
,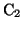 の両極板の電荷はそれぞれ
の両極板の電荷はそれぞれ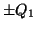 ,
,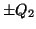 となった。
となった。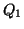 ,
,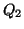 を求めよ。
を求めよ。

- (3)
- そのあとで,上記
 ,
, の操作をもう一度くり返した。このとき,コンデンサー
の操作をもう一度くり返した。このとき,コンデンサー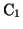 ,
,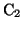 の両極板の電荷はそれぞれ
の両極板の電荷はそれぞれ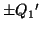 ,
,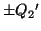 となった。
となった。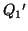 ,
,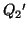 を求めよ。
を求めよ。

- (4)
- 上記
 ,
, の操作を
の操作を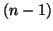 回くり返したときのP点の電位を
回くり返したときのP点の電位を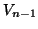 ,
,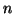 回くり返したときのP点の電位を
回くり返したときのP点の電位を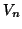 とするとき,
とするとき,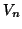 と
と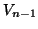 との関係を求めよ。ただし,接地点の電位を
との関係を求めよ。ただし,接地点の電位を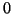 とする。
とする。

- (5)
- 上記
 ,
,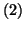 の操作を何度も繰り返すと,P点の電位はある値に近づいていく。どのような値に近づいていくか。
の操作を何度も繰り返すと,P点の電位はある値に近づいていく。どのような値に近づいていくか。

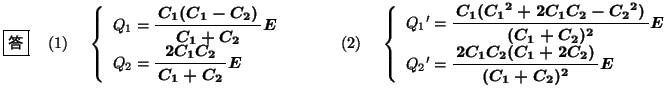
(3)
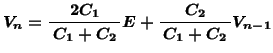 (4)
(4) ![]()
<攻略> コンデンサー回路の攻略法:
コンデンサー回路の問題では,まず並列,直列の式が使えないかどうかを検討する。この方法がだめな場合は,次の(a),(b)のいずれかの方法で考えていく。
![\begin{displaymath}
\colorbox{yellow}{%\begin{itembox}[l]{\hbox{$\ll${\textcol...
...d{array}} \right.$\end{enumerate}\end{enumerate}\end{itembox}}
\end{displaymath}](img32.gif)
 コンデンサー回路問題では,直列,並列の関係を使って解くのが最も簡単である。しかし,こうした考え方が適用できない場合は,より一般的な方法で解くしかない。その最も標準的な解法が,キルヒホッフの法則と電荷保存の法則を利用する方法である。また,キルヒホッフの法則と内容的には同じなのだが立式の形を少し変えた方法とし,電圧の代わりに電位を使って電荷を表す方法もある。
コンデンサー回路問題では,直列,並列の関係を使って解くのが最も簡単である。しかし,こうした考え方が適用できない場合は,より一般的な方法で解くしかない。その最も標準的な解法が,キルヒホッフの法則と電荷保存の法則を利用する方法である。また,キルヒホッフの法則と内容的には同じなのだが立式の形を少し変えた方法とし,電圧の代わりに電位を使って電荷を表す方法もある。
- (a)
- キルヒホッフの法則は回路問題を解く際の最も基本となる関係で,回路問題では何らかの形でキルヒホッフの法則が使われていると言って過言ではない。
![\begin{wrapfigure}[10]{r}{20zw}
\includegraphics [scale=1]{kaisetu1-1.eps}\end{wrapfigure}](img34.gif)
キルヒホッフの第2法則は,任意の閉回路において回路素子(抵抗やコンデンサー,電池など回路構成部品)にかかる電圧の合計が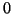 になるというものである。これをコンデンサー回路で利用する場合,次の手順でおこなう。
になるというものである。これをコンデンサー回路で利用する場合,次の手順でおこなう。
まずスイッチの切り替えを行う前の状態で,コンデンサーの接続部分の極板(図1の青色部分)に注目し,その帯電量を書き込む(図1の
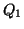 ,
,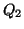 )。この場合,各極板の帯電量には正負の符号をしっかりと明記する。これを間違うとコンデンサー接続部分の帯電量和が違ってくるので,答が全く違ってくることになる。
)。この場合,各極板の帯電量には正負の符号をしっかりと明記する。これを間違うとコンデンサー接続部分の帯電量和が違ってくるので,答が全く違ってくることになる。
次にスイッチを切り替えたとき,接続部分の極板の新しい帯電量(図1の
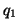 ,
,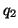 )を仮定する。この
)を仮定する。この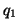 ,
,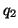 の正負は計算によって判明するのであって,現段階では不明である。したがって,
の正負は計算によって判明するのであって,現段階では不明である。したがって,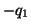 ,
,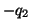 など,全く好きなように仮定しておけぱよい。よく,電池の正極につながった極板には必ず正電荷が帯電すると決め込んでいる諸君があるが,必ずしもそうなるとは限らない。直接続部分の帯電量和の値と電池の起電力によって
など,全く好きなように仮定しておけぱよい。よく,電池の正極につながった極板には必ず正電荷が帯電すると決め込んでいる諸君があるが,必ずしもそうなるとは限らない。直接続部分の帯電量和の値と電池の起電力によって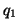 ,
,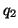 の正負が決まるのである。だからこそ,
の正負が決まるのである。だからこそ,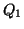 ,
,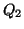 の正負は正しくつけておかたくてはならたいのである。
の正負は正しくつけておかたくてはならたいのである。
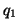 ,
,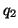 の正負は明らかではないが,立式の段階ではこれらはいずれも正の値という前提で式をたてていく。この仮定の下で,各コンデンサーの電位の高低がはっきりわかるように,図1に赤い破線で示したような三角形を描いていくとよい。三角形の広がっている方が高電位,三角形の先端の方が低電位と考え,時計回りでもよいし反時計回りでもよいから,三角形の向きにしたがって
の正負は明らかではないが,立式の段階ではこれらはいずれも正の値という前提で式をたてていく。この仮定の下で,各コンデンサーの電位の高低がはっきりわかるように,図1に赤い破線で示したような三角形を描いていくとよい。三角形の広がっている方が高電位,三角形の先端の方が低電位と考え,時計回りでもよいし反時計回りでもよいから,三角形の向きにしたがって をつけながら,各素子の電圧をすべて合計する。そして,その合計が
をつけながら,各素子の電圧をすべて合計する。そして,その合計が となるとおいていけばよい。たとえば図1の破線矢印の向きに合計する場合,
となるとおいていけばよい。たとえば図1の破線矢印の向きに合計する場合,
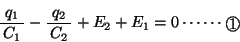
のように式を立てていく。これがキルヒホッフの法則を表す式である。一方,
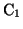 ,
,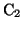 のコンデンサーの極板間は空気などの絶縁体で満たされていて,互いに相手極板との間で電荷の移動は起きない。つまり接続部分(図1の青部分)につながれた
のコンデンサーの極板間は空気などの絶縁体で満たされていて,互いに相手極板との間で電荷の移動は起きない。つまり接続部分(図1の青部分)につながれた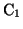 ,
,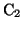 の極板は回路的に孤立しているのである。したがって,スイッチの切り替えで各極板の帯電量が変化しても,この接続部分の帯電量和は不変である。
の極板は回路的に孤立しているのである。したがって,スイッチの切り替えで各極板の帯電量が変化しても,この接続部分の帯電量和は不変である。
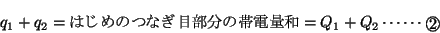
この 式と
式と 式から
式から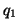 ,
,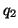 を求めていく。
を求めていく。
- (b)
- 1つのコンデンサーの2枚の極板には等量で正負の電気量が帯電するので,「コンデンサーの帯電量は?」といった場合,その大きさを指すことが普通である。その帯電量の大きさは
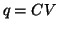 の式で与えられる。ここで
の式で与えられる。ここで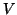 は電圧で,両極板の電,すなわち電位の差の絶対値である。
は電圧で,両極板の電,すなわち電位の差の絶対値である。
では,各極板の帯電量の正負まで含めた形で表すにはどのようにすればよいだろうか。そのためには,各極板の帯電量を電圧ではなく,電位を用いて次式のように表していくとよい。着目極板の帯電量=容量×(着目極板の電位−相手極板の電位)
![\begin{wrapfigure}[10]{r}{20zw}
\includegraphics [scale=1]{kaisetu2-2.eps}\end{wrapfigure}](img46.gif)
たとえば図2で極板A,Bの電位を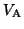 ,
,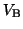 とすると,
とすると,

となり,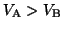 なら
なら
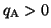 ,その逆なら
,その逆なら
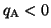 となる。高電位側が正に,低電位側が負に帯電するのは当然である。
となる。高電位側が正に,低電位側が負に帯電するのは当然である。
この方法を用いたコンデンサー回路の解法は次の手順で行う。
まず,コンデンサーの接続部分のはじめの帯電量を,
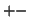 を付けて明記する。
を付けて明記する。
電位で考えていくので,電位 の点を決める。問題に接地点が記してあればその点の電位を
の点を決める。問題に接地点が記してあればその点の電位を とし,接地点が記してない場合は適当に自分で仮定する。この接地点を基準にして,判断し得る点の電位を書き込んでいく。
次に,スイッチの切り替えなどによって生じる新しい帯電状態を接続部分の極板について
とし,接地点が記してない場合は適当に自分で仮定する。この接地点を基準にして,判断し得る点の電位を書き込んでいく。
次に,スイッチの切り替えなどによって生じる新しい帯電状態を接続部分の極板について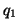 ,
,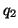 などと仮定し,同時に接続部分の電位
などと仮定し,同時に接続部分の電位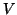 も仮定する。前述の(a)と同様に,現段階では
も仮定する。前述の(a)と同様に,現段階では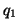 ,
,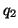 ,
,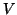 の正負は不明である。
の正負は不明である。
![\begin{wrapfigure}[10]{r}{20zw}
\includegraphics [scale=1]{kaisetu3-1.eps}\end{wrapfigure}](img53.gif)
このような仮定の下に,上に述べた方法で接続部分の極板の帯電量を表していく。
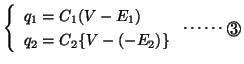
そして最後に,接続部分の電荷が保存されていることを表す式を立てる。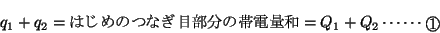
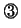 式を
式を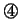 式に代入して
式に代入して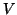 を求め,この
を求め,この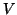 を
を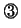 式に代入すると
式に代入すると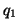 ,
,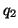 が求まる。実は,
が求まる。実は,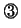 式から
式から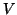 の文字を消去すると,前述(a)の
の文字を消去すると,前述(a)の 式になり,
式になり, 式はキルヒホッフの法則を2式に分割して記したにほかならないことが分かる。
式はキルヒホッフの法則を2式に分割して記したにほかならないことが分かる。
一般に(a)の解法は立式しやすいが,計算が面倒になる場合が多い。
<参考>そのほかに,並列連結と直列連結の重ね合わせとして考えていく「重ね合わせの原理」という解法もある。

- (1)
- スイッチをA側に入れると,
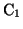 と
と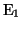 からなる閉回路ができ,
からなる閉回路ができ,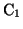 に
に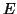 の電圧がかかる。
の電圧がかかる。
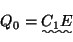
- (2)
- スイッチをB側に入れると,図4のような閉回路ができる。
このとき
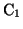 と
と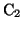 の接続部分(図の青色の部分)には
の接続部分(図の青色の部分)には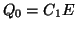 の電荷が帯電しているので,
の電荷が帯電しているので,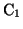 ,
,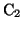 の直列連結の式を使って求めることはできない。
の直列連結の式を使って求めることはできない。
![\includegraphics [scale=1]{kaisetu4-1.eps}](img63.gif)
- (a)
- の解法: 図のように,
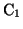 ,
,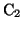 の接続部分P側極板の帯電量を
の接続部分P側極板の帯電量を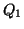 ,
,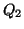 と仮定し,キルヒホッフの法則と電荷保存の式をたてると,
と仮定し,キルヒホッフの法則と電荷保存の式をたてると,
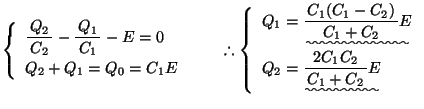
- (b)
- の解法: 接続部分P側極板の帯電量を図4のように仮定し,この部分の電位を
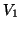 と仮定する。接地点の電位を
と仮定する。接地点の電位を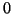 とすると,点aの電位は
とすると,点aの電位は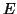 ,点bの電位は
,点bの電位は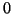 となる。図4で、各点の電位は( )を付して示した。
解法(b)にしたがって各極板の電荷と電荷保存の式をたてると,
となる。図4で、各点の電位は( )を付して示した。
解法(b)にしたがって各極板の電荷と電荷保存の式をたてると,
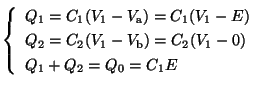
これより,
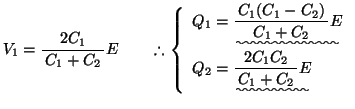
- (3)
- スイッチを再びA側に入れると,コンデンサー
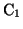 と電池
と電池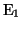 との閉回路ができ,
との閉回路ができ,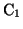 は再度
は再度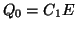 に充電され直される。一方
に充電され直される。一方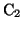 の方は前回の操作による電荷
の方は前回の操作による電荷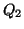 がそのまま残ることになる。よって図5のように
がそのまま残ることになる。よって図5のように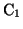 ,
,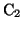 の接続部分の電荷を仮定すると,
の接続部分の電荷を仮定すると,
![\includegraphics [scale=1]{kaisetu5-1.eps}](img68.gif)
- (a)
- の解法: キルヒホッフの法則と電荷保存を表す式は,
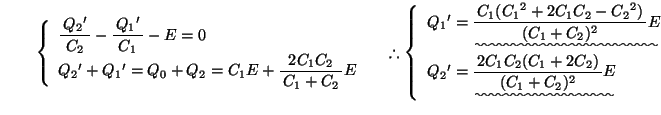
- (b)
- の解法:
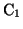 ,
,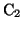 の接続部分の電位を
の接続部分の電位を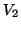 とすると,次の3式が成立する。
とすると,次の3式が成立する。
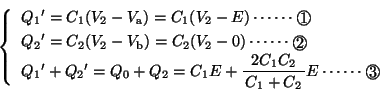
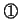 ,
,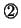 を
を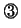 に代入して,
に代入して,
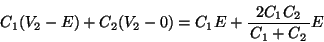
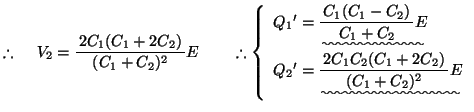
- (4)
- 本設問は,解法(b)で考えた方が考えやすい。
スイッチをAに入れるたびにコンデンサー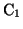 は
は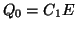 に充電され直される。一方
に充電され直される。一方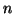 回目直前の
回目直前の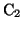 には1回前の電荷
には1回前の電荷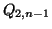 が残っている。よって,以下の3式が成立する。
が残っている。よって,以下の3式が成立する。
![\includegraphics [scale=1]{kaisetu6-1.eps}](img76.gif)
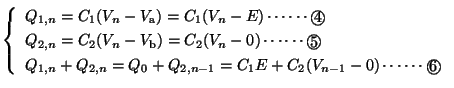
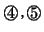 を
を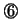 式に代入して,
式に代入して,
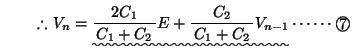
- (5)
- 無限回操作によって
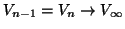 であるから,上式は,
であるから,上式は,
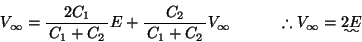
なお,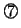 の漸化式を解くと,
の漸化式を解くと,
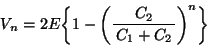
よって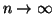 とおいて,
とおいて,