戻る　　 分野別一覧へ　　　　　トップページへ


慣性力詳解

　

慣性力－地上で見た運動と車内で見た運動の比較




　以下の図は、電車の天井から放たれた物体の運動軌跡を、地上の人（青色）が見た場合と、電車内の人（赤色）が見た場合の関係を示したものである。「>|」を押すとコマが進み、「|<」を押すとコマが戻ります。「加速」、「減速」、「等速度」を変更した場合は必ず「Reset」を押してください。 　




　また下の図は、加速中の電車の天井から、物体が静かに放たれた場合の解説図である。
　
　

\includegraphics[scale=1]{kanseiryoku-1.eps}


　
　 　電車の速度が$ v_0$のとき、物体は天井から離れたとする。それまでは電車と一緒に運動していたのだから、物体の地面に対する初速は$ v_0$である。
　その後物体には重力しかはたらかないので、地上で見た場合、物体は初速$ v_0$で投げ出された水平投射の放物運動をする。したがって物体の落下点をCとし、落下時間を$ t$とすると、この間の物体の地上から見た水平移動距離は $ \overline{\mathrm{AB}}=v_0t$である。
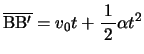　一方電車の加速度を$ \alpha$とすると、時間$ t$の間に電車は　 $ \overline{\mathrm{BB'}}=v_0t+\bun{1}{2}\alpha t^2$　の距離を進む。したがって電車内から物体を見ると、相対的に　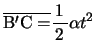 $ \overline{\mathrm{B'C}=}\bun{1}{2}\alpha t^2$　だけ左向きに移動している。すなわち電車内で物体を観測したとき、物体には左向きに$ \alpha$の加速度が生じているように観測されることになる。この加速度は電車の加速度、つまり電車に乗っている観測者の加速度と同じ大きさで逆向きである。
　したがってこの場合、この観測者から見ると、物体には左向きに　 $ f=m \alpha$　なる力がはたらいたように見えることになる。
　このように、加速度運動をしている観測者が観測したとき、実際にはたらいている力のほかにはたらいているように見える力を慣性力という。慣性力は運動学的に現れる力であるから、反作用を受ける相手物体はない。
　遠心力は円運動をしている観測者に対して現れる慣性力であり、さらに円運動をしている観測者に対して運動する物体に生じるコリオリの力というのも慣性力の一つである。