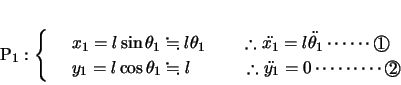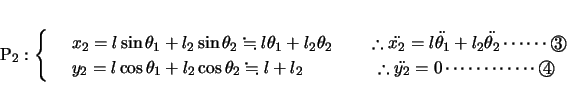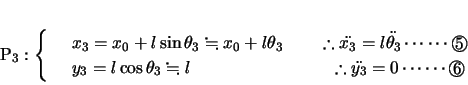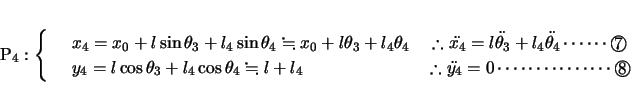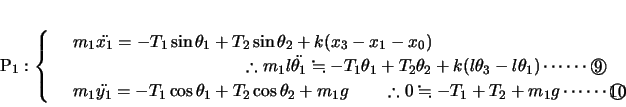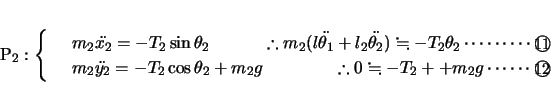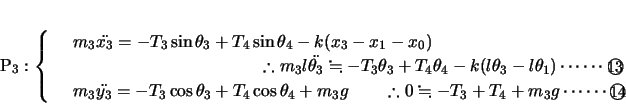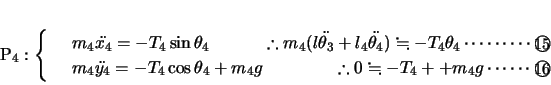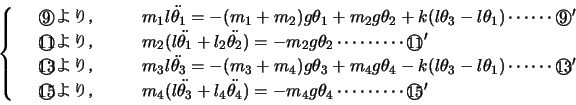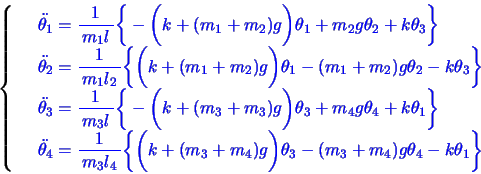下図において,天井の距離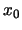 だけ離れた2点O,Rからそれぞれ第1小球
だけ離れた2点O,Rからそれぞれ第1小球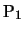 (質量
(質量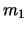 ),第3小球
),第3小球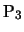 (質量
(質量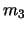 )がともに長さ
)がともに長さ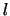 の糸(または針金)でつるされ,その下に第2小球
の糸(または針金)でつるされ,その下に第2小球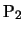 (質量
(質量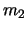 ),第4小球
),第4小球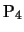 (質量
(質量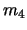 )がそれぞれ長さ
)がそれぞれ長さ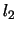 ,
,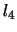 の糸で結ばれている。また,第1小球
の糸で結ばれている。また,第1小球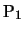 と第3小球
と第3小球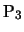 はばね定数
はばね定数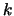 のばねで結ばれている。糸もばねもその質量は無視できる。
のばねで結ばれている。糸もばねもその質量は無視できる。
各小球の座標を図のようにとり,糸の張力を図のように表す。ただし各小球ともその変位は十分に小さく,糸が鉛直線に対してなす角
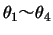 は十分に小さいとする。したがって,その変位は水平方向と近似できる。
は十分に小さいとする。したがって,その変位は水平方向と近似できる。
このとき各小球の変位,加速度(
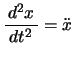 のように表記する)は以下のようになる。
のように表記する)は以下のようになる。
よって各小球の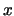 方向,
方向,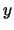 方向について運動方程式をたてると,
方向について運動方程式をたてると,
 より,
より, 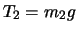
 より,
より,
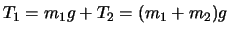
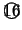 より,
より, 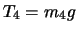
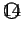 より,
より,
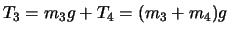
この関係を ,
,
 ,
,
 ,
,
 に代入して,
に代入して,
以上4式を連立させて,
以上の4式をもとにシミュレーションしたのが,先のアニメである。
![\includegraphics[scale=1.1]{furiko_kyousin_kaisetu2-1.eps}](img15.gif)
![\includegraphics[scale=1.1]{furiko_kyousin_kaisetu2-1.eps}](img15.gif)
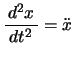 のように表記する)は以下のようになる。
のように表記する)は以下のようになる。