小球が鉛直面内で円運動しながら一周する条件


分野別一覧へ　　　　　トップページへ 　　　前に戻る

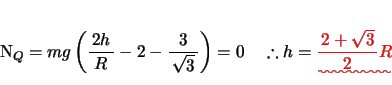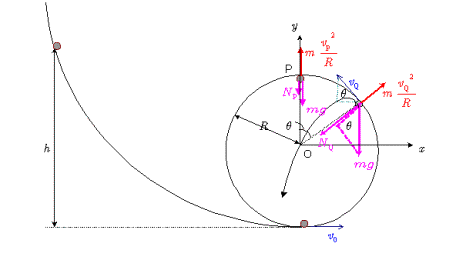
円形レールの中心Ｏより下方を運動中に、小球がレールから離れることがないことは自明であろう。したがって、Ｏ点よりの下の位置から小球を放した場合、小球は円形レールから離れることなく、レール上で往復運動をする事になる。円形レールの中心Ｏより上方から放した場合に、小球がレールか離れる可能性がある。

いま図において、円形レールの最下点からはかって高さ$h$の位置から小球が落下を始めたとする。このとき円形レールの最高点Ｐを通る鉛直線からはかって角$\theta $における小球の速さ$v_{} $は、力学的エネルギー保存則より、


\begin{displaymath} mgh = {\bun{{1}}{{2}}}mv_{} ^{2} + mgR(1 + \cos \theta )\qua... ...\left\{ {h - R(1 + \cos \theta )} \right\}}} \ldots \ldots (1) \end{displaymath}

よって小球がこの位置でレールから受ける垂直抗力$N$は、垂直抗力、重力、遠心力による半径方向のつりあいより、


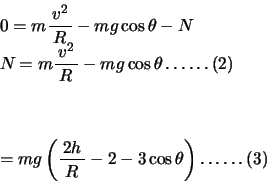
\begin{displaymath} \begin{array}{l} 0 = m{\bun{{v_{} ^{2}}}{{R}}} - mg\cos \th... ... - 2 - 3\cos \theta} \right)\ldots \ldots (3) \\ \end{array}\end{displaymath}

上式が、小球がレール上の任意の位置においてレールから受ける抗力の一般式である。

この垂直抗力$N$が小さいほど小球はレールから離れやすいことを意味し、その位置は上式より $\cos \theta = 0$となる位置、すなわちレールの最高点Ｐであることが分かる。したがって小球がレールに沿って完全に一周するためには、最高点Ｐにおいて垂直抗力が$0$以上であればよいので、$\theta = 0$で$N \ge 0$とおいて、


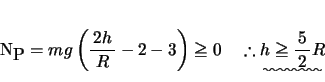
\begin{displaymath} % latex2html id marker 143N_{\mbox{P}} = mg\left( {{\bun{{... ...ight) \ge 0 \quad \therefore \uwave{h \ge {\bun{{5}}{{2}}}R } \end{displaymath}

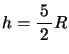であればよい。（ $h = {\bun{{5}}{{2}}}R$の点が点アである。）

つぎにレールから離れた小球が、その後放物運動してレールの中心Oを通る条件について考えてみよう。

小球がレールから離れる点をＱとする。点Ｑでの速さを$v_{Q} $とし、レールから離れてから中心Ｏに達するまでの時間を$t$とすると、水平方向、鉛直方向にそれぞれ放物運動の式を立てて、


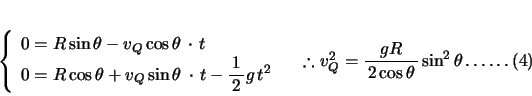
\begin{displaymath} % latex2html id marker 144{\left\{ {\begin{array}{l} {0 =... ...{\bun{{gR}}{{2\cos \theta}} }\sin ^{2}\theta \ldots \ldots (4) \end{displaymath}

一方$(2)$式で$N_{Q} = 0$とおいて、


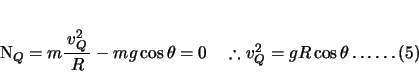
\begin{displaymath} % latex2html id marker 145N_{Q} = m{\bun{{v_{Q} ^{2}}}{{R}... ...\quad \therefore v_{Q} ^{2} = gR\cos \theta \ldots \ldots (5) \end{displaymath}

(4)と(5)より、


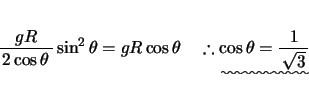
\begin{displaymath} % latex2html id marker 146\quad {\bun{{gR}}{{2\cos \theta}... ...ad \therefore \uwave{\cos \theta = {\bun{{1}}{{\sqrt {3}}} }} \end{displaymath}

これを$(3)$に代入して、


\begin{displaymath} % latex2html id marker 147N_{Q} = mg\left( {{\bun{{2h}}{{R... ...re h =\textcolor{red}{\uwave{{\bun{{2 + \sqrt {3}}} {{2}}}R }} \end{displaymath}