定　常　波 　詳解

戻る　　 分野別一覧へ　　　　　トップページへ

　時間が経っても移動しない波を定常波という。これに対して、時間経過ととともに移動していく一般の波のことを、定常波に対して「進行波」という。
　定常波がなぜ移動しないかというと、それは各点の振幅が場所によって決まっているからである。たとえば下図において、媒質各点は全て同じ振動数で振動しているが、点$\mathrm{A}$の振幅は$2a$、点$\mathrm{B}$の振幅は$a$、点$\mathrm{C}$の振幅は$0$、$\cdots \cdots$のように、各点の振幅が決まっているとする。ここである時刻において、媒質各点はそれぞれ各点の振幅に等しい最大変位をとっていて、波形$(\mathrm{a})$ようになっていたとする。その後時間の経過とともに媒質各点は、振幅の半分の値の変位、変位$0$、負の向きの最大変位、$\cdots \cdots$と振動を続けたとすると、その波形は図の $(\mathrm{a})\longrightarrow (\mathrm{b})\longrightarrow (\mathrm{c})\longrighta... ...)\longrightarrow (\mathrm{b}) \longrightarrow (\mathrm{a})\longrightarrow\cdots$のように変化する。

\includegraphics [scale=.67]{teizyo-eps1-2.eps}

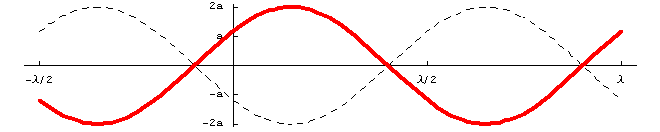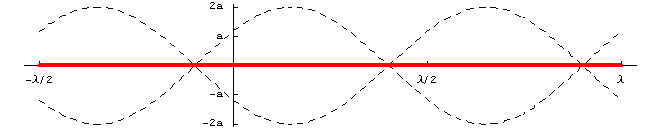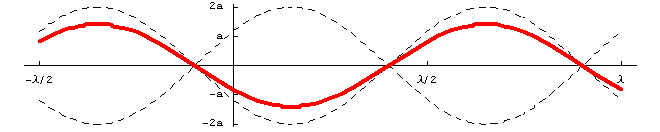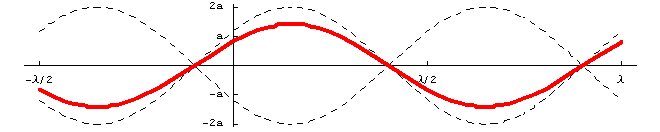
これより明らかなように、波形は時間とともに変化していくが、波形そのものの移動は見られない。これが定常波である。つまり定常波は、振幅が場所によって決まっていることによって移動しないように見えるのである。したがって定常波の数式上の特徴を書けば、振幅$A$が位置の関数になっていること（$A\small {(x)}$）、また媒質各点は単振動しているので、媒質各点の変位は時間の関数として表されること（ $y\varpropto f\small {(t)}$）である。このことより、定常波の一般的式は以下のように書き表すことができる。

\begin{displaymath}y\small {(x,t)}=A\small {(x)} \cdot f\small {(t)} \end{displaymath}


このように、定常波の数式上の特徴は、座標$x$のみを含む項（因子）と、時刻$t$のみを含む項（因子）とに分離され、その２つの積の形になることである。

さて、このような波は１つの単独の波では決してみられない。ではどのような場合にこのような波ができるかというと、振幅、波長、振動数に等しい波が互いに $\textcolor {red}{逆向きに進んだとき}$にのみ、見られるのである。この様子を、下のアニメで示してある。

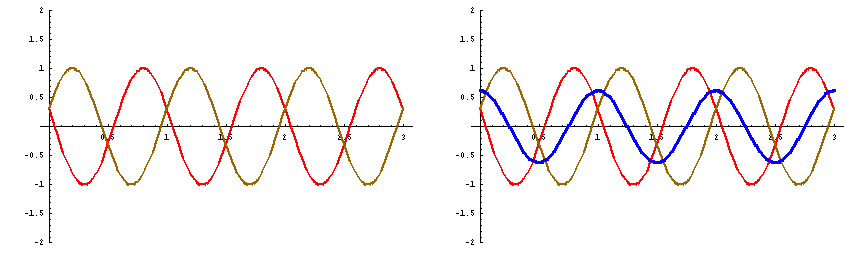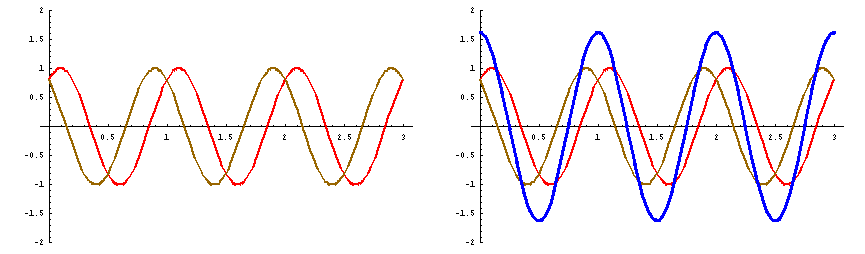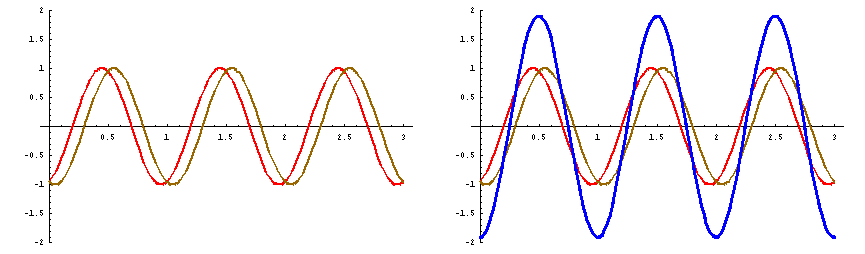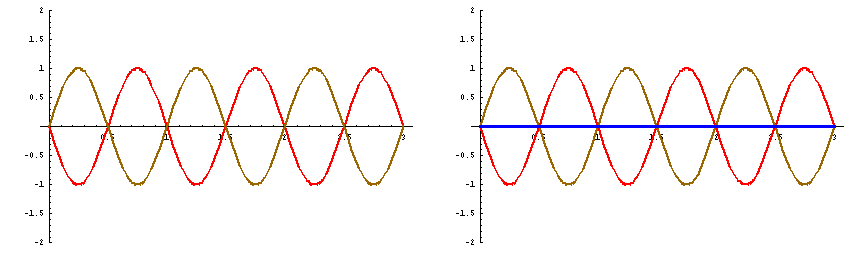
次にこのことを、数式を用いて示してみよう。
互いに逆進する２つの波を$y_1$、$y_2$とし、以下の式で表されるとする。

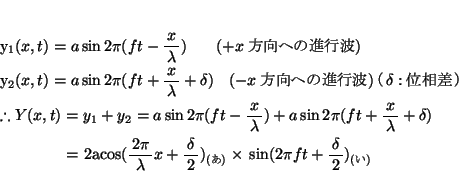
\begin{eqnarray*} % latex2html id marker 40y_1\small {(x,t)} &=& a \sin 2\pi (... ...ta}{2})_{(あ)} \times \, \sin (2\pi f t+\bun{\delta}{2})_{(い)} \end{eqnarray*}



以上より、合成波 $Y\small {(x,t)}$は、座標$x$のみの関数である$(あ)$項と、時刻$t$のみの関数である$(い)$項とに分離され、その積の形になっている。すなわち $Y\small {(x,t)}=A\small {(x)} \cdot f\small {(t)}$の形になっているので、これは定常波を表している。つまり、２つの等しい波が逆進するとき、その合成波は定常波となるのである。その振幅は$(あ)$項の絶対値として表され、

\begin{displaymath}A\small {(x)}=2a\bigg \vert \cos (\bun{2\pi}{\lambda}x+\bun{\delta}{2})\bigg \vert \end{displaymath}


となる。そして $A\small {(x)}=0$となる位置を $\textcolor{red}{節}$、 $A\small {(x)}=max$となる位置を $\textcolor{red}{腹}$という。