‘OӮЙ–ЯӮй Ғ@Ғ@ •Ә–м•КҲк——ӮЦҒ@Ғ@Ғ@Ғ@Ғ@ғgғbғvғyҒ[ғWӮЦ
Ғ@Ҳк”КӮЙ”gӮМ”ҪҺЛӮЙӮНҒCҲК‘ҠӮӘ![]() ӮёӮкӮйҢЕ’и’[”ҪҺЛӮЖҒCҲК‘ҠӮМӮёӮкӮИӮўҺ©—R’[”ҪҺЛӮЖӮӘӮ ӮйҒB
ӮёӮкӮйҢЕ’и’[”ҪҺЛӮЖҒCҲК‘ҠӮМӮёӮкӮИӮўҺ©—R’[”ҪҺЛӮЖӮӘӮ ӮйҒB
Ғ@ӮИӮЁҒC“§үЯ”gӮНҒCҲК‘ҠӮМӮёӮкӮрҗ¶Ӯ¶ӮИӮўҒB
Ғ@ҒғӮЬӮЖӮЯҒ„
![]()
![\begin{displaymath}
\colorbox{yellow}{%\begin{tabular}{\vert l\vert}
\hline \v...
...textcolor{red}{ҲК‘ҠӮМӮёӮкӮИӮө}\\ [3mm]
\hline
\end{tabular} }
\end{displaymath}](img3.gif)
Ғ@ӮўӮЬҒC![]() ҺІҸгӮр“`ӮнӮйӮPҺҹҢіӮМ”gӮӘӮ ӮйӮЖӮ·ӮйҒBӮҪӮҫӮөҒCҢҙ“_ӮnӮЕӮН”}ҺҝӮӘ•sҳA‘ұӮЙӮИӮБӮДӮЁӮиҒC
ҺІҸгӮр“`ӮнӮйӮPҺҹҢіӮМ”gӮӘӮ ӮйӮЖӮ·ӮйҒBӮҪӮҫӮөҒCҢҙ“_ӮnӮЕӮН”}ҺҝӮӘ•sҳA‘ұӮЙӮИӮБӮДӮЁӮиҒC![]() ӮЕӮН”}ҺҝҒi
ӮЕӮН”}ҺҝҒi![]() ҒjӮМ–§“xӮӘ
ҒjӮМ–§“xӮӘ![]() ҒC”gӮМ“`”А‘¬“xӮӘ
ҒC”gӮМ“`”А‘¬“xӮӘ![]() ҒC
ҒC![]() ӮЕӮН”}ҺҝҒi
ӮЕӮН”}ҺҝҒi![]() ҒjӮМ–§“xӮӘ
ҒjӮМ–§“xӮӘ![]() ҒC”gӮМ“`”А‘¬“xӮӘ
ҒC”gӮМ“`”А‘¬“xӮӘ![]() ӮЖӮ·ӮйҒB”gӮН
ӮЖӮ·ӮйҒB”gӮН![]() •ыҢьӮ©Ӯз“ьҺЛӮөҒCҢҙ“_ӮnӮЕ”gӮМҲк•”ӮӘ”ҪҺЛӮөҒCҺcӮиӮМҲк•”ӮНӮ»ӮМӮЬӮЬ
•ыҢьӮ©Ӯз“ьҺЛӮөҒCҢҙ“_ӮnӮЕ”gӮМҲк•”ӮӘ”ҪҺЛӮөҒCҺcӮиӮМҲк•”ӮНӮ»ӮМӮЬӮЬ![]() •ыҢьӮЦ“§үЯӮөӮДӮўӮӯҒB“ьҺЛ”gҒC”ҪҺЛ”gҒC“§үЯ”gӮрӮ»ӮкӮјӮкҒC
•ыҢьӮЦ“§үЯӮөӮДӮўӮӯҒB“ьҺЛ”gҒC”ҪҺЛ”gҒC“§үЯ”gӮрӮ»ӮкӮјӮкҒC
![\includegraphics[scale=.5]{wave-hansya-setumei-1.eps}](img15.gif)
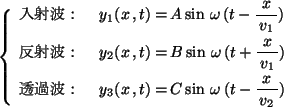
Ғ@ӮұӮұӮЕҒC
Ғ@ӮіӮДӮұӮМӮЖӮ«ӮұӮМ”}ҺҝҸгӮр”g“®ӮӘ“ьҺЛӮөӮДӮ«ӮҪӮЖӮ«ҒCҺҹӮМӮQӮВӮМҸрҢҸӮӘ–һӮҪӮіӮкӮДӮўӮИӮӯӮДӮНӮИӮзӮИӮўҒBӮВӮЬӮиҒC
- 1ҒK
- Ғ@”}ҺҝӮМ•ПҲКӮӘҒC
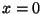 ӮМ“_ҒiӮQӮВӮМ”}ҺҝӮМҗЪ‘ұ“_ҒjӮЕҳA‘ұӮөӮДӮўӮИӮӯӮДӮНӮИӮзӮИӮўҒBҒi•ПҲКӮМҳA‘ұҗ«Ғj
ӮМ“_ҒiӮQӮВӮМ”}ҺҝӮМҗЪ‘ұ“_ҒjӮЕҳA‘ұӮөӮДӮўӮИӮӯӮДӮНӮИӮзӮИӮўҒBҒi•ПҲКӮМҳA‘ұҗ«Ғj
- 2ҒK
- Ғ@”}ҺҝҸгӮМӮ·ӮЧӮДӮМ“_ӮЕҒCғGғlғӢғMҒ[ӮМ•Ы‘¶‘ҘӮӘҗ¬—§ӮөӮДӮўӮИӮӯӮДӮНӮИӮзӮИӮўҒBҒiғGғlғӢғMҒ[ӮМ•Ы‘¶‘ҘҒj
ҒiғGғlғӢғMҒ[•Ы‘¶‘ҘӮМ‘гӮнӮиӮЙҒC•ПҲКӮМӢ——ЈҢщ”zӮМҳA‘ұҗ«ӮрҚlӮҰӮйӮМӮӘ•Ғ’КӮҫӮӘҒCҚӮҚZҗ¶ӮЙӮНғGғlғӢғMҒ[ӮМ•Ы‘¶‘ҘӮМ•ыӮӘ—қүрӮөӮвӮ·ӮўӮЖҺvӮнӮкӮйӮМӮЕҒCӮұӮұӮЕӮНӮ»ӮМ—§ҸкӮЕҗа–ҫӮ·ӮйҒBҒj
Ғ@ӮЬӮё1ҒKӮЙӮВӮўӮДҚlӮҰӮжӮӨҒB![]() ӮМ“_ӮЕӮМӮ»ӮкӮјӮкӮМ”g“®ӮЙӮжӮйҗU“®ӮНҒCҸгҺ®ӮЙ
ӮМ“_ӮЕӮМӮ»ӮкӮјӮкӮМ”g“®ӮЙӮжӮйҗU“®ӮНҒCҸгҺ®ӮЙ![]() Ӯр‘г“ьӮөӮДҒC
Ӯр‘г“ьӮөӮДҒC
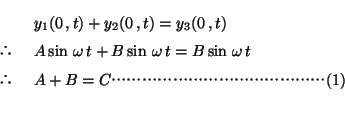
Ғ@ҺҹӮЙҒC2ҒKӮЙӮВӮўӮДҚlӮҰӮйҒB”g“®ӮӘ’PҲКҺһҠФӮЙү^ӮФғGғlғӢғMҒ[—КӮрҒC”gӮМӢӯӮіӮЖӮўӮӨҒB”gӮМӢӯӮі
Ғ@ӮжӮБӮД“ьҺЛ”gҒC”ҪҺЛ”gҒC“§үЯ”gӮМ”gӮМӢӯӮіӮрӮјӮкӮјӮк
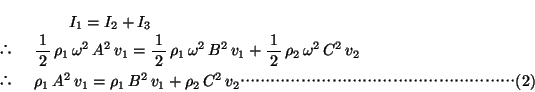
(1)ӮЖ(2)ӮрҳA—§ӮіӮ№ӮДҒC![]() ҒC
ҒC![]() Ӯр
Ӯр![]() ӮЕ•\Ӯ·ӮЖҒC
ӮЕ•\Ӯ·ӮЖҒC
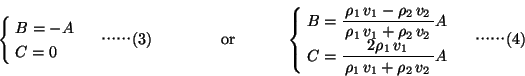
Ғ@(3)ӮН“§үЯ”gӮМҗU•қ![]() ӮӘ
ӮӘ![]() ӮЖӮўӮӨӮұӮЖӮЕҒC“–ҸүӮжӮ蓧үЯ”gӮр”Ы’иӮөӮДӮўӮйүрӮЕӮ ӮйӮ©ӮзӮұӮкӮН•s“KҒBӮжӮБӮД(4)ӮӘ
ӮЖӮўӮӨӮұӮЖӮЕҒC“–ҸүӮжӮ蓧үЯ”gӮр”Ы’иӮөӮДӮўӮйүрӮЕӮ ӮйӮ©ӮзӮұӮкӮН•s“KҒBӮжӮБӮД(4)ӮӘ![]() ҒC
ҒC![]() Ӯр—^ӮҰӮйҒB
Ӯр—^ӮҰӮйҒB
Ғ@ҲИҸгӮжӮиҒC![]() ҒC
ҒC![]() ӮМ‘еҸ¬ӮЙӮ©Ӯ©ӮнӮзӮё
ӮМ‘еҸ¬ӮЙӮ©Ӯ©ӮнӮзӮё![]() ӮЕӮ ӮиҒC
ӮЕӮ ӮиҒC
Ғ@ӮөӮ©ӮөҒC”ҪҺЛ”gӮН![]() ҒC
ҒC![]() ӮМ‘еҸ¬ӮЙӮжӮБӮДҒCҺҹӮМӮQӮВӮМғPҒ[ғXӮӘӮ ӮйҒB
ӮМ‘еҸ¬ӮЙӮжӮБӮДҒCҺҹӮМӮQӮВӮМғPҒ[ғXӮӘӮ ӮйҒB

- —бӮP
- Ғ@Ң·ҸгӮр“`ӮнӮйүЎ”gӮМҸкҚҮҒF
Ғ@Ң·Ӯр“`ӮнӮйүЎ”gӮМ‘¬Ӯі
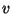 ӮНҒCҢ·ӮМ’Ј—НӮр
ӮНҒCҢ·ӮМ’Ј—НӮр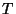 ҒCҢ·ӮМҗь–§“xӮр
ҒCҢ·ӮМҗь–§“xӮр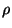 ӮЖӮ·ӮйӮЖҒC
ӮЖӮ·ӮйӮЖҒC
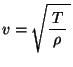 ӮЖӮўӮӨҺ®ӮЕ—^ӮҰӮзӮкӮйӮдӮҰҒC
ӮЖӮўӮӨҺ®ӮЕ—^ӮҰӮзӮкӮйӮдӮҰҒC
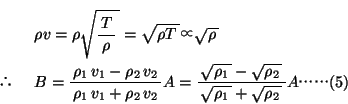
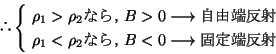
- —бӮQ
- Ғ@ү№”gҒiҸc”gҒjӮМҸкҚҮҒF
Ғ@Ғ@ӢуӢCӮЕҒCҒ@Ғ@
 ҒC
ҒC
Ғ@Ғ@җ…ӮЕҒCҒ@Ғ@Ғ@
 ҒC
ҒC
Ғ@Ғ@Ғ@
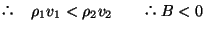
Ғ@ӮВӮЬӮиӢуӢC’ҶӮ©Ӯзҗ…’ҶӮЙү№”gӮӘ“ьҺЛӮ·ӮйҸкҚҮҒC”ҪҺЛү№”gӮНҢЕ’и’[”ҪҺЛӮЖӮИӮйҒB
- —бӮR
- Ғ@Ңх”gӮМҸкҚҮҒF
Ңх”gӮМҸкҚҮӮНҒCҸгӢLӮМӢcҳ_ӮрӮ»ӮМӮЬӮЬ“–ӮДӮНӮЯӮйӮұӮЖӮНӮЕӮ«ӮИӮўӮМӮЕҒCӮ ӮӯӮЬӮЕӮаӮ»ӮМ—Юҗ„ӮЖӮөӮД—қүрӮөӮДӮЁӮўӮДӮўӮҪӮҫӮ«ӮҪӮўҒB
Ғ@Ңх”gӮНүЎ”gӮдӮҰҒCҢ·ӮМҸкҚҮӮр“–ӮДӮНӮЯӮДҚlӮҰӮжӮӨҒB‘OӢL(5)Һ®ӮЙӮЁӮўӮДҒC
Ғ@Ғ@
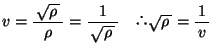 Ғ@
Ғ@
ӮМҠЦҢWӮрҺgӮБӮД
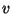 ӮМҺ®ӮЙҸ‘Ӯ«’јӮ·ӮөҒCӮіӮзӮЙ
ӮМҺ®ӮЙҸ‘Ӯ«’јӮ·ӮөҒCӮіӮзӮЙ
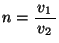 ӮрӮаӮБӮД
ӮрӮаӮБӮД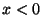 ӮМ—МҲжӮМ”}ҺҝӮЙ‘ОӮ·Ӯй
ӮМ—МҲжӮМ”}ҺҝӮЙ‘ОӮ·Ӯй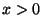 ӮМ—МҲжӮМӢьҗЬ—ҰӮЖ’иӢ`Ӯ·ӮкӮОҒC
ӮМ—МҲжӮМӢьҗЬ—ҰӮЖ’иӢ`Ӯ·ӮкӮОҒC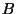 ҒCӮЁӮжӮС
ҒCӮЁӮжӮС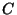 ӮНҺҹӮМӮжӮӨӮЙӮИӮйҒB
ӮНҺҹӮМӮжӮӨӮЙӮИӮйҒB
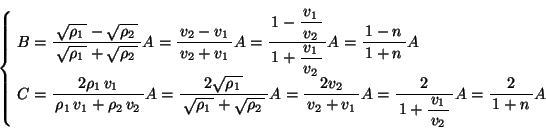
Ғ@ӮұӮМӮұӮЖӮ©ӮзҒCӢьҗЬ—Ұ
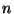 ӮӘ
ӮӘ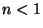 ӮИӮзӮО
ӮИӮзӮО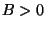 ҒCӮВӮЬӮи”ҪҺЛ”gӮН“ьҺЛ”gӮЖ“ҜҲК‘ҠҒC
ҒCӮВӮЬӮи”ҪҺЛ”gӮН“ьҺЛ”gӮЖ“ҜҲК‘ҠҒC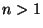 ӮИӮзӮО
ӮИӮзӮО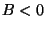 ҒCӮВӮЬӮи”ҪҺЛ”gӮН“ьҺЛ”gӮЙ‘ОӮөӮДҲК‘ҠӮӘ
ҒCӮВӮЬӮи”ҪҺЛ”gӮН“ьҺЛ”gӮЙ‘ОӮөӮДҲК‘ҠӮӘ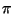 ӮёӮкӮйҒBӮұӮкӮЙ‘ОӮөӮДҒC
ӮёӮкӮйҒBӮұӮкӮЙ‘ОӮөӮДҒC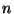 ӮМ’lӮЙӮжӮзӮё
ӮМ’lӮЙӮжӮзӮё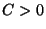 ӮЕӮ ӮйӮ©ӮзҒC“§үЯ”gӮМҲК‘ҠӮНӮёӮкӮйӮұӮЖӮНӮИӮўҒB
ӮЕӮ ӮйӮ©ӮзҒC“§үЯ”gӮМҲК‘ҠӮНӮёӮкӮйӮұӮЖӮНӮИӮўҒB
ӮұӮМӮұӮЖӮрҒCҢх”gӮрҠЬӮЮүЎ”gҲк”КӮЙӮВӮўӮДӮЬӮЖӮЯӮйӮЖҺҹӮМӮжӮӨӮЙӮИӮйҒB
![\begin{displaymath}
\colorbox{yellow}{%\begin{tabular}{\vert l\vert}
\hline \v...
...ҶC•ўж]ж·дCб®–ҝеў—ўҚўжў•ўҢ@яя} \\ [3mm]
\hline
\end{tabular} }
\end{displaymath}](img52.gif)