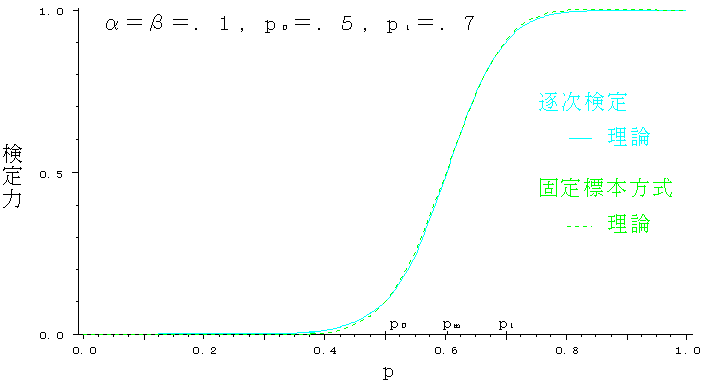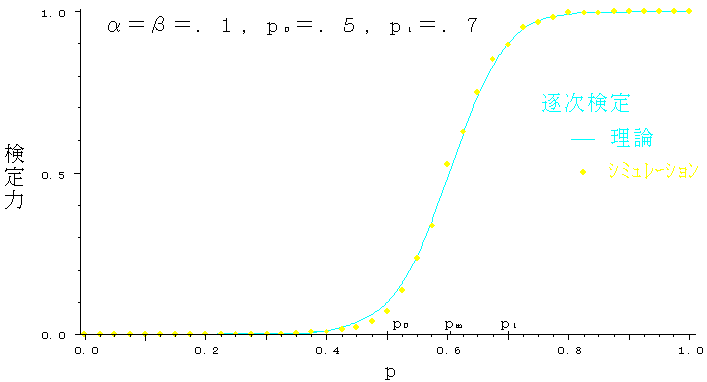電子情報通信学会技術研究報告, ET92-88, pp.21-28, 1992-12-12
逐次検定の学習評価への適用について
小林 修
|
あらまし 2つの単純仮説に対する逐次検定は,固定標本方式に較べて標本数が半減することが知られている.しかし,連続量である学習水準を評価する場合,無限個の仮説を同時に検定することになり,逐次検定をそのままの形で適用することができない.本稿では,この問題を「学習水準pがp0程度か,p1程度か」と読み代えることにより,学習水準の評価に逐次検定が有効であることを,シミュレーションにより示す.この検定では,被験者の学習水準pが,p0以下のときはH0が,p1以上のときはH1が,ほとんどの場合に採択され,pが両者の中間にあるときは,H0またはH1が確率的に採択される.固定標本方式に比した平均標本数は,5〜8割程度に削減される.
|
1.まえがき
逐次検定は,固定標本方式に較べて,標本数が少なくてすむという利点がある.例えば,硬貨投げの表裏の確率が0.5と0.7のいずれであるかを検定する場合,2種類の過誤をともに0.10とすると,0.7が真の場合,固定標本方式では39試行,途中で打ち切っても平均34試行を要するが,逐次検定では平均21試行で検定が終了する(3.4参照).
しかし,一般に逐次検定は,この例のように,2つの単純仮説に対して定式化されているので,このままの形で連続量である学習水準の評価に適用することはできない.学習水準を評価する場合,すべての学習水準に対応した無限個の単純仮説を立てることになるからである.
本稿では,逐次検定を学習水準の評価に適用する際の考え方,およびその際の逐次検定の振る舞いについて,数値計算およびシミュレーションによって明らかにする.
なお,米軍の訓練データによる実際的研究の報告が文献(4)に,また項目反応理論に基づいたテスト項目を使用して逐次検定を行なった場合および項目反応理論による能力推定との現実的な比較研究が文献(3)pp.237-283に報告されている.
2.学習水準とカテゴリ
本稿では,何らかの測度で測った量に従って,被験者をいくつかのカテゴリに分類することを考えているのだが,被験者の能力をどのようなモデルで記述するかは,難しい問題である.
ごく一般的に考えれば,所与の課題に取り組むということは,被験者が,既存の内的モデルの総体を組み直し,課題に対応できる内的モデルを再構築する試みであると考えることができる.適切な内的モデルの構築に成功すれば,解答が得られるわけである.内的モデルの再構築は相当に劇的なプロセスと考えられるから,正答率50%等という中間的な学習程度は考えにくい.むしろ,解答できるかできないかの二者択一のように思われる.しかし,一般に学習目標は,特定の問題の解答そのものにあるのではなく,より抽象的なレベル(学習内容の汎化)にあるのが普通であり,再構築される内的モデルも,より一般的なものが期待されている.学習内容の汎化とは,その内的モデルの一般化の程度に他ならない.
このように考えると,「ある被験者の,あるテスト項目に対する正答率」という概念は余り意味を持たず,「ある学習目標に対応する一群のテスト項目に対して,正答可能なテスト項目の割合」と考える方が妥当であるように思われる.本稿でいう正答率は,このような意味で使われている.
この意味で,1年次では30%,2年次では60%,3年次では80%,などの年次別の習得目標を設定することができる.本稿でいうカテゴリ分けは,このような状況を想定したものである.
3.逐次検定
この章では,逐次検定の概要について述べる.この章の議論は,特定点θm(3.2参照)における検定力と平均標本数の導出を除き,主として文献(1)-(2)による.
記号については,各節の「記号および定義」の項にまとめてあるので,随時参照されたい.
3.1 逐次検定の概要
逐次検定では,一般の検定のように標本数をあらかじめ固定することをせず(3.4参照),標本を得るたびに,検定仮説H0と対立仮説H1の尤度を算出し,その比λが,グレイゾーン(採択限界c1と棄却限界c2の間)
c1 < λ < c2
にある限り判定を保留し,サンプリングを続ける.上記の範囲を越えたときに検定は終了するが,当然そのときの標本数は一定ではない.検定に要する標本数は,同じ第1種,第2種の過誤α,βをもつ固定標本方式に比べ,概ね半数程度になることが知られている.
c1,c2とα,βの関係式は,それぞれの仮説H0,H1が正しく判定される確率1−α,1−βを定義に従って劣評価することにより,得られる.詳細は,文献(1)を参照されたい.
また,θの真の値がθ0とθ1の間にあるときには,逐次検定がいつまでも終わらない印象を受けるが,検定が終わらない確率は0であることが示されている(2).
記号および定義
| | 母集団(θ)の確率密度 | | f(x;θ) |
| 検定仮説 | H0:θ=θ0 |
| 対立仮説 | H1:θ=θ1 |
| 検定仮説H0の確率密度 | f0(x)=f(x;θ0) |
| 対立仮説H1の確率密度 | f1(x)=f(x;θ1) |
| 第1種の過誤 | α |
| 第2種の過誤 | β |
| 尤度比 | |
| 採択限界 |
|
| 棄却限界 |
|
3.2 検定力関数と平均標本数
この節の検定力関数および平均標本数の導出法は,θmにおける値の導出を除いて,すべて文献(2)pp.232-236によるものである.ただし,記号は,一部異なっている.また,陰関数の微分法や微分積分の交換,可積や極限値の存在の条件などは適当に揃っているものと仮定しておく.
検定力関数P(θ)は,母数θに対して,検定仮説H0を棄却する確率である.定義により,P(θ0)=α,P(θ1)=1−βである.
記号および定義
| | 検定力関数 | | P(θ) |
| 平均標本数 | | E[n](θ) |
|
| E[z](θ) =∫z(x)f(x;θ)dx |
| E[z2](θ)=∫z(x)2f(x;θ)dx |
| θmの定義: | | E[z](θm)=0 |
| φ(u;θ)=∫( | f1(x) | )u | f(x;θ)dx |
|
| f0(x) | |
| h(θ)の陰関数定義: | | φ(h(θ);θ)=1
但し,h≠0(図1参照) |
3.2.1 検定力関数の導出
本稿に必要な点のみ,概要を述べる.詳細は,文献(2)を参照されたい.
関数g(x;θ)を次のように定めると,
| | g(x;θ)=( | f1(x) | )h(θ)f(x;θ) | (1) |
|
| f0(x) |
h(θ)の定義により,g(x;θ)を確率密度と考えることができる.すると,所与の逐次検定をf(x;θ)とg(x;θ)に関する採択限界 c1h 棄却限界 c2h の逐次検定に読み代えることができ,これから第1種の過誤を逆算して,次の検定力関数を得る.
ここで,この導出法では,h(θ)=0のときは,(1)式で定義される確率密度g(x;θ)がf(x;θ)と一致し,fとgが逐次検定を構成しない,よって,(2)式を直ちに適用することができないことに注意されたい.(このことは,(2)式の分母が0になることからも了解される.)
さて,φ(u;θ)は,その定義から,次の性質を持つことがわかる.
φ(0;θ)=1
φ ′(0;θ)=E[z](θ)
u→±∞ のとき φ(u;θ)→∞
図1は,この様子を描いたものである.このことから,
θ→θm のとき h(θ)→0
であり,(2)式からP(θm)を求めることができないことがわかる.
P(θm)は,P(θ)のθ→θmでの極限を取ることにより求められる.
| P(θm)= | −logc1 | (3) |
|
| logc2−logc1 |
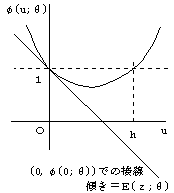
図1 関数φ(u;θ)の概形とh(θ)の定義(2)
3.2.2 平均標本数の導出
平均標本数の導出は長くなるので,結果だけを引用する(2).
| E[n](θ)= | P(θ)logc2+(1-P(θ))logc1 | (4) |
|
| E[z](θ) |
ここで,上式の形から(また,ここでは述べないが,導出の手順からも),E[z](θ)=0のとき,即ちθ=θmのとき,上式はそのままでは適用できない.
E[n](θm)は,再び,E[n](θ)のθ→θmでの極限をとることにより求められるが,この際,(4)式の分母だけでなく,(3)式から分子もまた0になることに注意されたい.逐次検定はθ0とθ1の差が大きいほど有利であるという直感は事実と一致するが,母数θが両者の中間(≒θm)にあるときに平均標本数E[n](θ)が発散するという直感は,(4)式によって直ちに裏付けられるわけではないのである.
実際,長く間違い易い計算を注意深く行なえば,次式が得られる.
| E[n](θm)= | (−logc1)(logc2) | (5) |
|
| E[z2](θm) |
上式の分母は,明らかに真正値であり,従ってE[n](θm)が発散することはない.
この直感と事実との乖離の解釈については,4.2で再考する.
3.3 二項分布の場合
本稿では,二項分布を仮定しているので,前節までの結果のいくつかを,二項分布の形式で,以下にまとめておく.
記号および定義
| | 正答率(母数θ) | | p |
| 誤答率 | q=1−p |
| 母集団の確率密度 | f(x;p)=pδ(正)(x)+qδ(誤)(x) |
| 検定仮説 | H0:p=p0 |
| 〃 の誤答率 | q0=1−p0 |
| 対立仮説 | H1:p=p1 |
| 〃 の誤答率 | q1=1−p1 |
| pmの定義:E[z](pm)=0 |
定義により,pmは次のようになる.
| pm= | −(logq1−logq0) |
|
| (logp1−logp0)−(logq1−logq0) |
また,(5)式および簡単な計算により,次のE[n](pm)を得る.
| E[n](pm)= | (−logc1)(logc2) |
|
| (logp1−logp0)(−logq1+logq0) |
3.4 固定標本方式
前節の問題を固定標本方式で検定する場合については,周知のことであろうが,簡単に触れておく.
n回の試行に対する確率密度をfn(x;p)とすれば(xは正答した回数),
fn(x;p)=pxqn-x (0 ≦ x ≦ n)
であり,与えられた過誤α,βに対する所要標本数Nは,p0<p1とすれば,
∫c∞fN(x;p0)dx=α
∫-∞cfN(x;p1)dx=β
を,N,cについて解き,求めることができる.ここに現れたcはH0の採択限界を表している.
例えば,1.で挙げた例と同じα=β=0.10,p0=0.5,p1=0.7とすれば,N=39,c=24となる.即ち,硬貨投げの場合,39回の試行のうち表を24回以上観測したら,H0 を棄却し,H1を採択することとなる.
ここで注意したいのは,表を24回観測した時点でH0棄却という検定結果が確定することである.同様に,裏を16回観測すれば,39試行で表が24回以上観測されることはなく,H0が採択されることがその時点で確定する.こうして,標本数を削減することができる.1.で示した平均標本数34は,このように扱った場合のシミュレーションによって求めた数値である.なお,以下の本文および図中の「打ち切りあり」は,この扱いを示している.この「打ち切り」については,4.1で,再度考察する.
4.逐次検定の学習評価への適用
この章では,2.で述べた考え方に従い,被験者をある測度で測った学習水準によって,2つのカテゴリに分類することを考え,これに逐次検定を適用し,固定標本方式と比較する.
学習水準は,0〜1の実数で表され,任意のテスト項目に対する正答率に一致するものとする.ここでは,偶発による正答は考慮しない.
以下では,α=β=0.10とする.また,実際のテスト項目での観察から,2つのカテゴリ間の正答率の差は,0.1〜0.2と想定される.従って,以下では,p0=0.5,p1=0.6とp0=0.5,p1=0.7の2つのケースについて考察する.
4.1 平均標本数
平均標本数の理論値およびシミュレーションによる実測値を,表1,図2,図3に掲げる.
3.2.2で指摘したように,pがp0とp1の中間にあっても平均標本数は発散しない.逐次検定が最も不利となるpm付近においてさえ,固定標本方式(打ち切りあり)に比較して,なお8割程度に削減され,有効性を保っている.しかも,|p0−p1|= 0.1 のときの方が 0.2のときより削減幅は大きくなっている.
この事実は,逐次検定が有効なのは,一般にいわれているように|p0−p1|が十分大きいとき,ではないことを示している.
図2,図3から,固定標本方式でも,打ち切りを行なうと,かなり標本数を削減できるケースがあることがわかる(グラフの両裾).もし打ち切りをしなかった場合は,39(p1=0.7の場合)の標本を要することになるが,その標本からはpを推定することができる.それに反し,打ち切りを行なった場合は,結果としてpの推定を放棄し,標本の持つ情報量をH0とH1の二者択一に縮約する.その代わりに,標本数の削減という利益を得ているのである.
実際,得られた標本からpを推定する問題を考えてみよう.pが0〜1のいずれかの値をとる可能性が一様であるとすれば,標本から計算される「標本p(以下psと記す)」を生ずる母数pの可能性を逆算することができる.図4,図5は,そのpの可能性(ps=0,1/3,1の3つのケース)および(情報量の大きさの指標として)標準偏差を示したものである.図2と対照すれば,前述の解釈を裏付けていることが看取される.(図5の横軸は,pではなく psであることに注意されたい.)
逐次検定の場合は,更に徹底して,pの推定はほとんど不可能であり,その分,標本数は,少なくてすむのである.
以上の考察から,逐次検定は,偏った標本に対してサンプリングを停止することにより平均標本数を削減しているのであり,|p0−p1|の大きさには直接関係していないことがわかる.|p0−p1|は,E[n](p)のグラフの尖度に関係しているのである.従って,pがp0,p1の中間にあるから平均標本数が発散するという直感は成り立たないのである.
以上から,pがp0,p1に関わりなく分布すると考えねばならない学習水準の評価にも,逐次検定は十分に効果があると結論できる.
| p0=0.5, p1=0.7,|p0−p1|= 0.2 | |
|
| 逐次検定 | 固定標本方式 |
|
|
| p | 理論(比*) | シミュレーション | シミュレーション |
|
| p0 | 20.2(.65) | 18.5 | 31.3 |
| pm(.603) | 28.1(.81) | 28.4 | 34.9 |
| p1 | 21.4(.64) | 20.5 | 33.6 |
| 全平均** | 12.8(.49) | 12.8 | 26.2 |
|
| 所要標本数N=39 |
| p0=0.5, p1=0.6,|p0−p1|= 0.1 | |
|
| 逐次検定 | 固定標本方式 |
|
|
| p | 理論(比*) | シミュレーション | シミュレーション |
|
| p0 | 86.1(.57) | 89.5 | 151.1 |
| pm(.550) | 118.7(.75) | 125.3 | 158.6 |
| p1 | 87.3(.58) | 82.7 | 151.6 |
| 全平均** | 34.2(.30) | 35.2 | 115.1 |
|
| 所要標本数N=168 |
|
| | α=0.1,β=0.1 |
| | *固定標本方式に対する比. |
| | **全平均欄は,pに関する平均の概数. |
表1 平均標本数の主な値
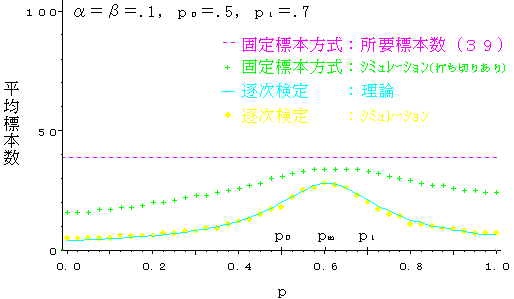
図2 平均標本数(p0=0.5,p1=0.7)
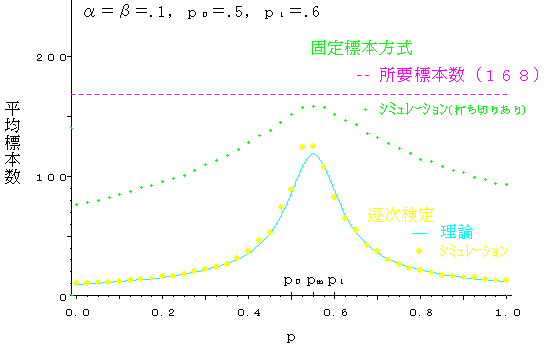
図3 平均標本数(p0=0.5,p1=0.6)
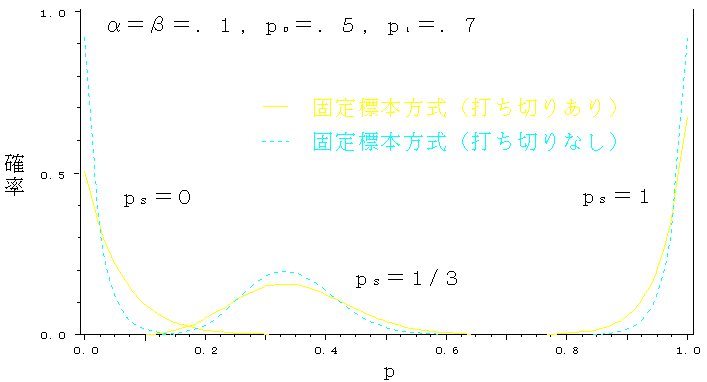
図4 pの推定(p0=0.5,p1=0.7)
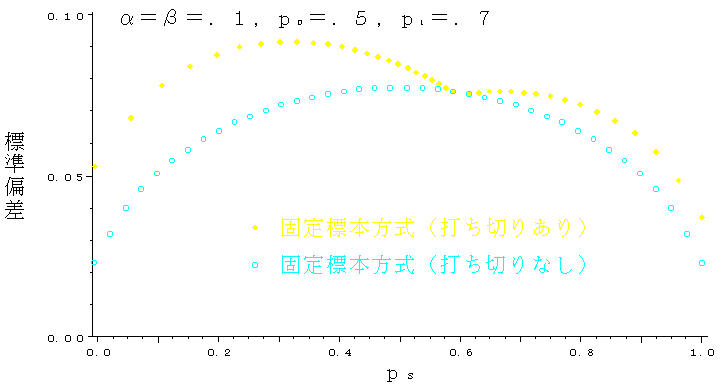
図5 pの推定値の情報量(p0=0.5,p1=0.7)
4.2 検定力
逐次検定と固定標本方式の検定力関数(理論値)を図6に示す.一見して明らかなように両者は極めて近似している.実際,両者の差は最大でも 0.01 程度しかない.この近似の程度は|p0−p1|= 0.1 のときも同様である.
これは,p0とp1を代表値とするカテゴリ分け問題について,逐次検定と固定標本方式は,検定能力の上で,差がないことを意味する.
また,逐次検定の検定力のシミュレーションによる実測値を図7に示す.理論値と非常によい一致を示している.
両図中のp0とp1およびpmの位置から観察されるように,この検定によって,被験者は,およそpmを境に2つのカテゴリに分類される.その検定結果は確率的であり,H1(上位群)と判定される確率は,定義によりP(p)である.
被験者の学習水準pがp0とp1の外側にあるときは,ほとんどの場合,下位群(H0)または上位群に分類されるが,両者の間にあるときはどちらにも判定され得る.しかし,両図の検定力関数の形から,この検定が幾度も実施されるなら,その採択率から検定力関数を逆に辿って,pが推定できることがわかる.
この事実は,3.2.2で指摘した疑問に説明を与えるものである.即ち,直感的には,pがp0とp1の中央付近にあるときは,標本が平均的に現れて,尤度比が両採択限界の内で振れることになり,逐次検定がいつまでも終了しないと思われるが,これは事実と異なる点である.事実は,4.1で述べたように,pがp0とp1の中央付近にあっても検定は終了する.この場合,尤度比がいつまでも振れるのではなく,上述のように,検定結果が振れるのである.例えば,α=βのときのpmにおける検定力P(pm)は 0.5 であるから,尤度比が有限回の振れで収束する代わりに,検定力が最も弱くなっていることが了解できる.
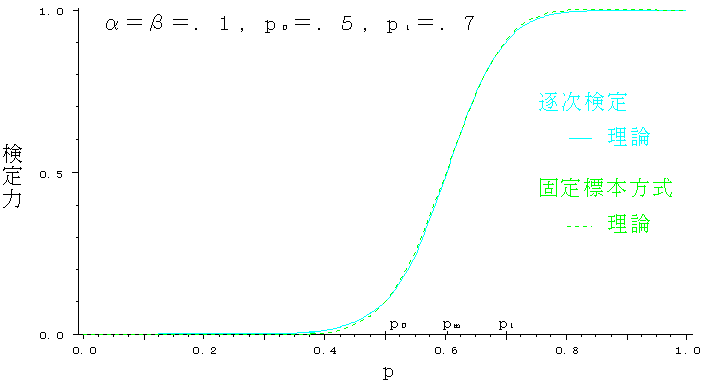
図6 検定力の比較(p0=0.5, p1=0.7)
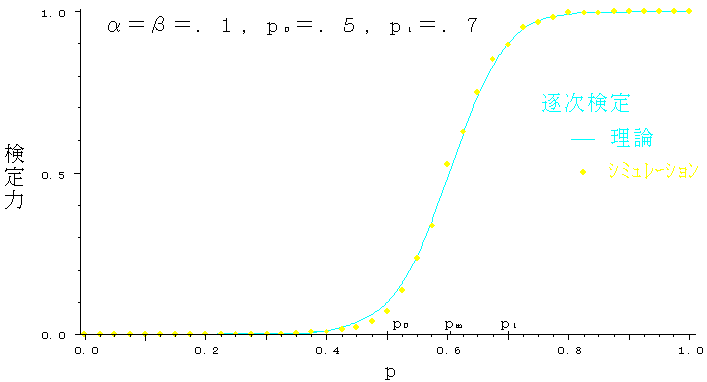
図7 検定力(p0=0.5, p1=0.7)
4.3 学習評価への適用
前二節で述べたことから,p0,p1の値に関わらず,またpの全域にわたって,逐次検定は,固定標本方式より,平均標本数に関して有利であり,学習評価への適用が可能であることがわかる.
次に,カテゴリ分け問題への適用について考える.
前節で述べた検定力関数の形状は,一般に,“pがpm以上か,pm以下か”という検定問題に逐次検定を適用する際の根拠とされる.例えば,到達度の検定で60%を達成基準とするような場合である.この場合,2つの複合仮説の検定であるから,2つの単純仮説を検定する逐次検定はそのままの形では適用できない(以下,固定標本方式でも同様).
これを,未達成の上限p0と達成の下限p1を設定し,“p=p0か,p=p1か”という検定として,逐次検定を適用する.こうすると,前節で述べた検定力関数の形状から,この検定は“pがpm以上か,pm以下か”という検定問題の解答にもなっているのである.
しかし,この解釈は,p0,p1の設定に関する理論的根拠に乏しいことが,弱点となっている.
これに対し,本稿では,“上位群(基準値p=p1),下位群(基準値p=p0)という2つのカテゴリへの分類問題”として,この問題を解釈することにする.
何故なら,検定力関数が階段状である(両側が平坦になっている)ことは,pの順序性から生じたもので,逐次検定に固有の性質ではないからである.実際,逐次検定を3つ以上の仮説の検定に拡張することができるが,当然予想されるように,その場合には,検定力関数(各検定仮説の採択率)は階段状になるとは限らないのである(5).
図8に,p=0.15,0.25,0.40,0.60,0.75を基準値とする5つのカテゴリへの分類問題に対する,逐次検定の振る舞いを示す.同図から,逐次検定を母数(p)が連続であるような複合仮説に適用したとき,この検定が,実際に,カテゴリ分けをしている様子がよくわかる.
この解釈は,2.で述べた学習評価の考え方に適合するものである.
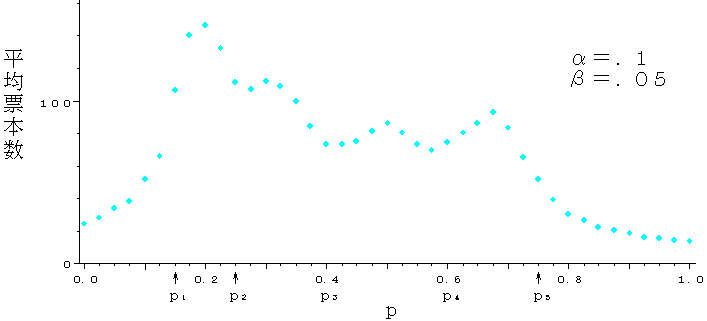
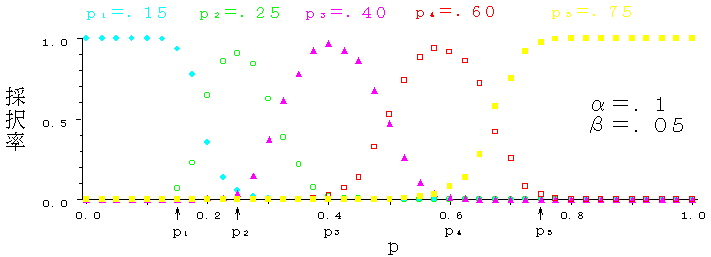
図8 5つのカテゴリへの分類
5.むすび
以上,逐次検定の有効性および複合仮説への適用について,一般に流布されている解釈(その中には,明白な誤りを含むものがある)とは多少異なる解釈を提示し,これを学習評価に適用する際の留意点および有効性について述べた.
逐次検定は,“紙と鉛筆の試験”では制約が強すぎ,実現性に乏しいが,コンピュータ支援が可能であれば,出題形式等に制約があるものの,ランダム逐次出題は極めて容易である.この分野への逐次検定の適用は,コンピュータ支援によって初めて実効性が生じたといっても良い.また,多様な困難度を持つテスト項目を用意できれば(これにはコンピュータ支援が必須である),平均標本数のピークをならすことができ,更に有効となる(5).
パーソナル・コンピュータが普及している現状に鑑み,適切なるアセスメントの下に,有効活用されることを望むものである.
文献
| | (1) | P.G.ホーエル:“入門数理統計学”,培風館(1990-9). |
| | (2) | 河田龍夫,国沢清典:“現代統計学”,廣川書店(1972-9). |
| | (3) | Weiss D.J.(ed.):“New horizons in testing : latent trait test theory and computerized adaptive testing”, Academic Press,New York(1983). |
| | (4) | Epstein K.I., Knerr C.S.:“Applications of sequential testing procedures to performance testing”, Proceedings of the 1977 Computerized adaptive testing Conference(1978). |
| | (5) | 小林修:“適応型逐次検定システムの開発”,信学技報,ET92-22,pp.5-12(1992-5). |
Copyright (C) 1997 by KOBAYASHI Osamu. All rights reserved.