]> アルゴリズムイントロダクション第 9 章中央値と順序統計量 (その 1)

中央値と順序統計量 (その 1)

nanto_vi (TOYAMA Nao)

予定

順序統計量とは
選択問題とは
最小値と最大値
平均線形時間選択アルゴリズム
最悪線形時間選択アルゴリズム

順序統計量とは

i 番目の順序統計量: i 番目に小さい要素
最小値: 1 番目の順序統計量
最大値: n 番目の順序統計量
中央値: $\frac{n + 1}{2}$ 番目の順序統計量 (n が奇数); $\frac{n}{2}$ 番目 (小さいほうの中央値) と $\frac{n}{2} + 1$ 番目 (大きいほうの中央値) の順序統計量 (n が偶数)

選択問題とは

順序統計量を求める問題
ここでは集合の要素はすべて異なると仮定
選択問題を解く
- ソートした結果の i 番目を返す
  - 計算時間は $O (n \lg n)$
- i が特定の値なら O ⁡ n で解ける
  - $i = 1$ (最小値)、 $i = n$ (最大値)
- 一般の選択問題の場合は?

最小値と最大値

最小値 (最大値) のみを求める

$n - 1$ 回の比較で結果が求まる
実行時間は $Θ (n)$

$\begin{aligned} Minimum (A) \\ 1 & \min \leftarrow A [1] \\ 2 & for i \leftarrow 2 to length [A] \\ 3 & do if \min > A [i] \\ 4 & then \min \leftarrow A [i] \\ 5 & return \min \end{aligned}$

最小値と最大値を同時に求めるには

別々に求める
- 1 要素に対して 2 回の比較
- 全体で $2 n - 2$ 回の比較
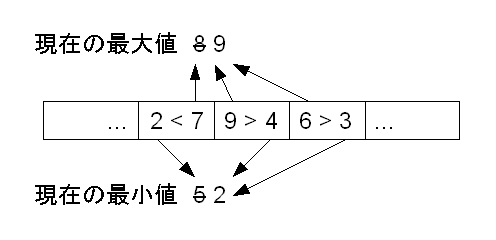
要素を対にし、まず対の中で比較
- 2 要素に対して 3 回の比較
- 全体で $3 ⌊\frac{n}{2}⌋$ 回の比較

対の中で比較し、その小さいほうを現在の最小値と、大きいほうを現在の最大値と比較する。

平均線形時間選択アルゴリズム

乱択アルゴリズム
平均実行時間が線形 ( $O (n)$ )

$\begin{aligned} Randomized-Select (A, p, r, i) \\ 1 & if p = r \\ 2 & then return A [p] \\ 3 & q \leftarrow Randomized-Partition (A, p, r) \\ 4 & k \leftarrow q - p + 1 \\ 5 & if i = k \\ 6 & then return A [q] \\ 7 & elseif i < k \\ 8 & then return Randomized-Select (A, p, q - 1, i) \\ 9 & else return Randomized-Select (A, q + 1, r, i - k) \end{aligned}$

実行時間の評価

Randomized-Select の実行時間を $T (n)$ とする。

ところで、 $\begin{array}{l} X_{k} := I \{部分配列 A [p .. q] がちょうど k 個の要素を持つ\} \\ = I \{A の中で k 番目に小さい要素がピボットとなる\} \end{array}$ とすると、 $\begin{array}{l} E [X_{k}] = \Pr \{A の中で k 番目に小さい要素がピボットとなる\} \\ = \frac{1}{n} \end{array}$

Randomized-Select の 1 回の呼び出しにおける実行時間は、 $\begin{array}{l} T (n) \leq \sum_{k = 1}^{n} X_{k} \cdot (T (\max (k - 1, n - k)) + O (n)) \\ = \sum_{k = 1}^{n} X_{k} \cdot T (\max (k - 1, n - k)) + O (n) \sum_{k = 1}^{n} X_{k} \\ = \sum_{k = 1}^{n} X_{k} \cdot T (\max (k - 1, n - k)) + O (n) \end{array}$

この期待値は、 $\begin{array}{l} E [T (n)] \leq E [\sum_{k = 1}^{n} X_{k} \cdot T (\max (k - 1, n - k)) + O (n)] \\ = \sum_{k = 1}^{n} E [X_{k} \cdot T (\max (k - 1, n - k))] + O (n) \\ = \sum_{k = 1}^{n} E [X_{k}] \cdot E [T (\max (k - 1, n - k))] + O (n) \\ = \sum_{k = 1}^{n} \frac{1}{n} \cdot E [T (\max (k - 1, n - k))] + O (n) \\ = \frac{1}{n} (\sum_{k = 1}^{⌈\frac{n}{2}⌉} E [T (n - k)] + \sum_{k = ⌈\frac{n}{2}⌉ + 1}^{n} E [T (k - 1)]) + O (n) \\ \leq \frac{1}{n} (\sum_{k = 1}^{⌈\frac{n}{2}⌉} E [T (n - k)] + \sum_{k = ⌊\frac{n}{2}⌋ + 1}^{n} E [T (k - 1)]) + O (n) \\ = \frac{1}{n} (\sum_{k = ⌊\frac{n}{2}⌋ + 1}^{n} E [T (k - 1)] + \sum_{k = ⌊\frac{n}{2}⌋ + 1}^{n} E [T (k - 1)]) + O (n) \\ = \frac{2}{n} \sum_{k = ⌊\frac{n}{2}⌋}^{n - 1} E [T (k)] + O (n) \end{array}$

右辺第 2 項はある定数 a を用いて $a n$ で抑えられる。ここで、ある定数 c に対して $E [T (n)] \leq c n$ 、ある定数 d に対して $n < d$ で $T (n) = O (1)$ と仮定すると、 $\begin{array}{l} E [T (n)] \leq \frac{2}{n} \sum_{k = ⌊\frac{n}{2}⌋}^{n - 1} c k + a n \\ = \frac{2 c}{n} (\sum_{k = 1}^{n - 1} k - \sum_{k = 1}^{⌊\frac{n}{2}⌋ - 1} k) + a n \\ = \frac{2 c}{n} (\frac{(n - 1) n}{2} - \frac{(⌊\frac{n}{2}⌋ - 1) ⌊\frac{n}{2}⌋}{2}) + a n \\ \leq \frac{2 c}{n} (\frac{(n - 1) n}{2} - \frac{(\frac{n}{2} - 2) (\frac{n}{2} - 1)}{2}) + a n \\ = \frac{3 c n}{4} + \frac{c}{2} - \frac{2}{n} + a n \\ \leq \frac{3 c n}{4} + \frac{c}{2} + a n \\ = c n - (\frac{c n}{4} - \frac{c}{2} - a n) \\ = c n - (\frac{c - 4 a}{4} n - \frac{c}{2}) \end{array}$

ここで、 $c > 4 a$ とすると、 $n \geq \frac{4}{c - 4 a} \frac{c}{2} = \frac{2 c}{c - 4 a}$ で $E [T (n)] \leq c n$ だから、 $E [T (n)] = O (n)$