（２−１）第２章 低エネルギー集束イオンビーム装置
２−１．緒言
集束イオンビーム直接蒸着法を実現するための最大の技術的課題が、集束されかつ低エネルギーのビームをいかにして得るかにあることは前章において述べた。したがって、低エネルギー集束イオンビーム装置（３０〜２００ｅＶにおいて微細なビーム径の金属ビームが得られる装置）を設計製作し、直接蒸着可能な集束イオンビームを得ることが、集束イオンビーム直接蒸着法実現のために第一に取り組むべき課題であった。
低エネルギーの集束イオンビーム装置を作成する試みは、浅いイオン注入および基板に対する損傷を抑えるための低エネルギーイオン注入を目的として、Pease等およびGamo等が１９８８年頃より開発をおこなっている１〜３）。特にPease等は対物レンズとターゲット基板を対向させ、ターゲット基板に直接減速電位を印加することにより、ビーム径が１μｍに迫る低エネルギーＧａ＋ビームが得られることを初めて報告し、低エネルギー集束イオンビームを実現することを妨げる決定的な要因がないことを示した。著者のめざした集束イオンビーム装置は、Pease等の実験装置をさらに発展させ、１μｍ以下のビーム径を持つ低エネルギービームを実現するとともに、合金イオン源と質量分離器による多種のイオン種の利用、広範囲における偏向電極および試料ステージを用いた描画、超高真空雰囲気における成膜、光学顕微鏡組み込みによる試料表面の実時間観察、搬送用チェンバーによる短時間の基板交換等の機能を持つ、集束イオンビーム直接蒸着法の基本的な実証と同時に、実用的な直接蒸着法の応用研究にも耐えうるものである
低エネルギー集束イオンビームを得るためのイオン光学系の設計にあたって、まずその系の光学特性（ビーム径等）をあらかじめ何らかの手法により評価し、求められる性能のイオンビームが得られるかどうかを予測することが必要になる。一般に集束イオンビームの場合、ごく低電流の領域をのぞいてビーム径は線源径と倍率により決まる理想的な値ではなく、光学系の持つ収差により決定される。収差には球面収差、色収差、幾何収差等いくつかの種類がある。それらのうちで光学特性に大きな影響を与えると思われる主要な成分について評価することによって、光学特性を予測することが可能となる。その手段は、荷電粒子光学系シミュレーション（simulation）技術と呼ばれ、通常光学系部品のつくりだす電磁界を計算する部分、および得られた電磁界の分布よりビーム径を評価する部分の二つの部分により構成される。電磁界の計算は解析的な手法で解ける特殊な形状をのぞいて、数値計算によりおこなう。その手法には、差分法、有限要素法、表面電荷法、電荷重畳法などが用いられる。ビーム径を評価する手法には、大きく分けて近軸近似に基づき解析的な手法から導き出される収差係数の算出よりビーム径の評価をおこなう手法と、電磁界中で一つ一つの荷電粒子の運動方程式を解きモンテカルロ（Monte Carlo）法との併用によりビーム径の評価をおこなう手法の二つの手法がある。
集束イオンビームの場合、レンズ系は軸対称でありターゲットに到達するビームの軌道が中心軸より大きくはずれることはない。したがって近軸近似が有効に適用できるため、収差係数によるビーム径の評価方法が有効である。低エネルギー集束イオンビーム光学系（レンズ系）の設計にあたって、有限要素法により電界分布を計算し、収差係数の算出によりビーム径を評価するプログラムを作成した。このプログラムは与えられたレンズ系の形状、配置、電位より倍率、軸上球面収差係数および軸上色収差係数の算出をおこなう。その結果得られる予想ビーム径を吟味しながら形状、配置等を修正し、繰り返し評価することにより低エネルギー集束イオンビームを得るために最適な条件を探索し、最終的に設計に採用し得る解を得た。
本章においては、光学系評価手法（シミュレーション手法）の概要および計算結果、それに基づいて設計製作した低エネルギー集束イオンビーム装置の概要を述べた後、実際にその装置により得られた低エネルギー集束イオンビームについて測定結果をまとめ、光学系について考察する。
２−２．光学系評価手法
光学系評価手法として用いたものは、Munroが発表した手法、およびプログラム４）を原形とし、これをもとに修正、改良を加えてたものである５〜７）。この手法は、レンズの倍率、軸上球面収差、軸上色収差を計算し、ビーム径を評価する。
この手法は、大きく分けて４つの部分より構成される。最初の部分は、与えられたレンズ形状と電位より、有限要素法を用いて中心軸上の電位分布Ｖ（ｚ）を求める。イオンビームの進行方向をｚ軸とし、線源位置をｚｏ、焦点位置をｚｉとする。使用した有限要素法は軸対称を前提とした極座標による２次元の計算である。
２番目の部分は、線源位置から焦点位置に至る中心軸上の電位Ｖ（ｚ）をに基づき、初期条件
（２−１）
および
（２−２）
で、次に示す近軸軌道方程式を、４次のRunge-Kutta法により解く。ｒ'はｒのｚに対する１階微分、ｒ''は２階微分、Ｖ'はＶのｚに対する１階微分、Ｖ''は２階微分を示す。
（２−３）
焦点位置を固定した計算においては、想定焦点位置で焦点を結ぶようレンズの電位等を調節する必要がある。つまり、計算したい焦点位置において次の条件を満たさなければならない。
（２−４）
このようにして、収差を評価する上で必要な基準軌道ｒ(ｚ)が得られる。またここで、倍率Ｍが求められる。線源と焦点面が同電位の時には、式（２−２）より
（２−５）
であるが、線源と焦点面の電位が異なるときには、Helmholtz-Lagrangeの公式より、次のようになる。
（２−６）
３番目の部分では、中心軸上電位分布Ｖ(ｚ)および基準軌道ｒ(ｚ)に基づき、ビーム径を評価するための収差係数の計算をおこなう。
レンズにより集束されたイオンビームの焦点における直径をｄとすると、ｄはレンズの倍率Ｍ、実効的な線源径ｄｏ、球面収差により決まるビーム径ｄＳ、および色収差により決まるビーム径ｄＣにより、次のようにあらわされる。
（２−７）
これはさらに、焦点面でのビーム半角をαｉ、球面収差係数をＣＳ、イオンビームの最終エネルギーをＥ、エネルギー幅をΔＥ、色収差係数をＣＣとおくとき、次のようにあらわされる。
（２−８）
球面収差係数ＣＳおよび色収差係数ＣＣはそれぞれ次のようにあらわされる。
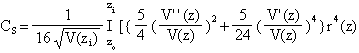
（２−９）
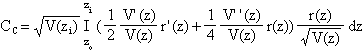（２−１０）
これらの式により、Ｖ(ｚ)、ｒ(ｚ)、あるいはそれらのｚ軸に対する微分をもちいて収差係数を算出する。
最後に、倍率と収差係数を用いて、式（２−８）により、ビーム径を算出する。エネルギーＥは、最終電位Ｖ(ｚｉ)に対応する。焦点面での半角αｉは、線源における角電流密度ＪΩと計算したいビーム電流値Ｉにより計算される。線源から一定の角電流密度で発生したビームを、ある電流値に対応する立体角で切り出し、この部分のみが焦点面に到達するという条件を想定している。線源面におけるビームの半角αｏは、
（２−１１）
とあらわされる。式（２−６）に示したように、αｏとαｉの関係は、倍率Ｍを用いて、
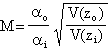（２−１２）
となるため、この二つの式を用いてαｉは次のようにあらわされる。
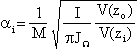（２−１３）
このようにして、ビーム径の評価をおこなうことができる。
原形となったMunroのプログラムに対する修正点は、ビーム径計算部分も含めてすべて単一プログラムで連続しておこなえるようにしたこと、複数のレンズを一つの複合レンズ系として取り扱えるようにしたこと、収差係数の積分時に積分の間隔が粗いと特に減速場において大きな誤差を招くために８）、区間を適当に設定し区間内の積分間隔を任意に設定できるようにしたこと等である。
低エネルギーイオンビームの場合、空間電荷の影響によりビーム径が影響を受けることが考えられるが、これに対してもPease等が評価をおこなっている９）。その報告によれば最終エネルギーが５００ｅＶであってもビーム電流が１００ｐＡ以下であれば、ビーム径に影響はない（≪０．１μｍ）。また彼等の実験結果においてもエネルギー５０ｅＶ、電流値９００ｐＡのＧａ＋ビームにおいて線幅１〜１．５μｍを報告しており２）、計算による評価を裏付ける結果となっている。したがって、著者の光学系においてもビーム径が決定的な影響を受けるとは考えられないため、空間電荷の影響に関しては独自な評価はおこなっていない。