曲率と曲率半径
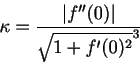
で表されます。 曲率の逆数のことを曲率半径といいます。例えば、直線の曲率は0だったので、曲率半径は無限大ということになります。直線は半径無限大の円だったのです。つまり、微分法が曲線を接線近似しているのに対し、曲率を求めることは曲線を円近似しているということになります。面白いのでこの曲率を力学の問題に応用してみます。
今、質量  従って |
曲率と曲率半径
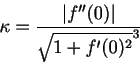
で表されます。 曲率の逆数のことを曲率半径といいます。例えば、直線の曲率は0だったので、曲率半径は無限大ということになります。直線は半径無限大の円だったのです。つまり、微分法が曲線を接線近似しているのに対し、曲率を求めることは曲線を円近似しているということになります。面白いのでこの曲率を力学の問題に応用してみます。
今、質量  従って |