まずはフェルマーの原理から

フェルマーの原理とは「光は最短光路を通る」という幾何光学において最も基本的な法則です。 数式で表せば

\begin{displaymath} \delta \int_A^B nds = 0 \end{displaymath}

ただしnは屈折率で、∫ndsは光路長です。実は解析力学はここから生まれた学問です。 物体が運動してある状態からある状態（力学では状態は位置と速度で指定されます）に移ったとき もしかしたら何かが最小となるように運動していたのではないか？光の光路長が最小となっていたように。 実はそのような量は存在していて、「作用」と呼ばれています。従って力学においても、 「物体（系）は作用が最小となるように運動する。」といえます。これを最小作用の原理あるいは ハミルトンの原理といって、光学のフェルマーの原理に対応するものです。式で書くと
\begin{displaymath} \delta \int_{t_1}^{t_2} L dt = 0 \end{displaymath}

ただし、Lはラグランジアンで、∫Ldtが作用です。ラグランジアンって何って思うかもしれませんが、 ここでは後回しにさせてください。ただそういうものがあるんだくらいに思っていてください。今言えることはラグランジアンは位置と 速度、そして時間の関数だということくらいです。

いよいよラグランジュの運動方程式を導出

今度は最小作用の原理から出発しましょう。簡単のため扱う系は１次元としますが多次元でも話は同じです。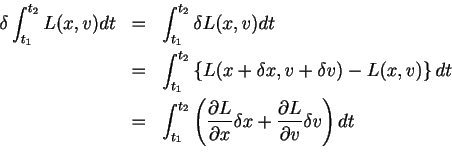

\begin{eqnarray*} \delta \int_{t_1}^{t_2}L(x,v)dt & = & \int_{t_1}^{t_2} \delta ... ...x}\delta x +\frac{\partial L}{\partial v}\delta v \right) dt\\ \end{eqnarray*}

ここでδv=δ(dx/dt)=(d/dt)δx、およびδx(t1)=δx(t2)=0、δv(t1)=δv(t2)=0 （最後のは使わない）などに気をつけて計算を進めていくと

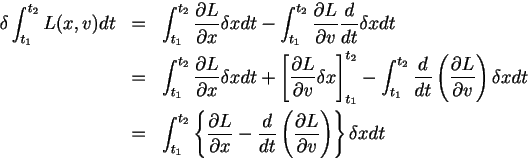\begin{eqnarray*} \delta \int_{t_1}^{t_2} L(x,v)dt& = &\int_{t_1}^{t_2} \frac{\p... ...left( \frac{\partial L}{\partial v} \right) \right\}\delta x dt \end{eqnarray*}

これが０となるのが最小作用の原理なのだから｛‥｝の中身が０になって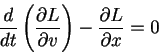

\begin{displaymath} \frac{d}{dt} \left( \frac{\partial L}{\partial v} \right)-\frac{\partial L}{\partial x}=0 \end{displaymath}

この方程式をラグランジュの運動方程式といってニュートンの運動方程式と完全に等価です。また xがn次元の時には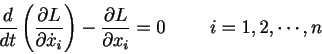

\begin{displaymath} \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}_i} \right)-\frac{\partial L}{\partial x_i}=0　　i=1,2,\cdots ,n \end{displaymath}

さらに座標系を変換した一般座標系でも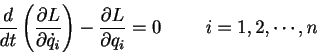

\begin{displaymath} \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right)-\frac{\partial L}{\partial q_i}=0　　i=1,2,\cdots ,n \end{displaymath}