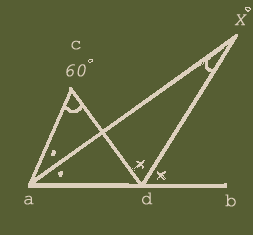
Ｍａｔｈ

　この二つの問題では、「三角形の二角の和は、残りの角の外角に等しい」という定理を使います。

問1

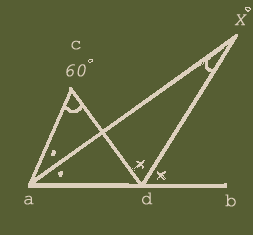　直線ａｂ上に三角形ａｃｄがあり、∠ａｃｄは６０°である。
　∠ｃａｂと∠ｃｄｂ、それぞれの角の二等分線が交わった点Ｘの角度を求めよ。


　答：∠Ｘ＝３０°

　解法：　　

図１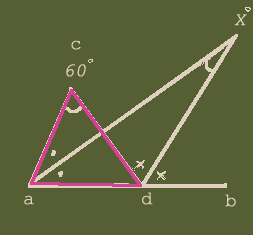

図２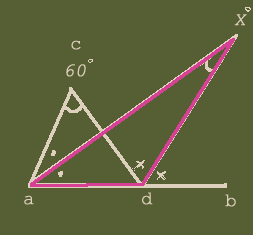

（図１）三角形ａｃｄで見ると、∠ａｃｄ＋∠ｃａｄ＝∠ｃｄｂ　つまり、　６０°＋２（∠・）＝２（∠×）
　　　　両辺を２で割って、３０°＋（∠・）＝（∠×）
　　　　移項して、　　　　３０°＝（∠×）-（∠・）　……（1）
（図２）三角形ａｄｘで見ると、∠ａｘｄ＋∠ｘａｄ＝∠ｘｄｂ　つまり、　∠Ｘ°＋（∠・）＝（∠×）
　　　　移項して、　　　　∠Ｘ°＝（∠×）-（∠・）
　　　（1）を代入して、　　∠Ｘ°＝３０°


問2

　∠ａ ＋ ∠ｂ ＋ ∠ｃ ＋ ∠ｄ ＋ ∠ｅ ＝　？


　答：１８０°

　解法：

図１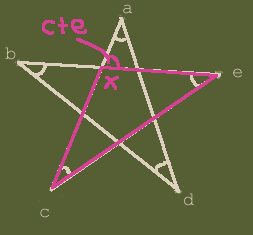

図２

図３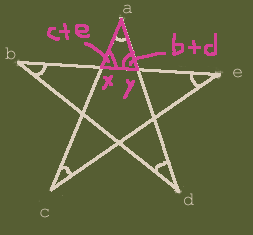

（図１）三角形ｘｃｅで見ると、∠ｘの外角は∠ｃ＋∠ｅに等しい……（1）
（図２）三角形ｙｂｄで見ると、∠ｙの外角は∠ｂ＋∠ｄに等しい……（2）
（図３）三角形ａｘｙの内角の和は、（1）と（2）より、∠ａ＋（∠ｃ＋∠ｅ）＋（∠ｂ＋∠ｄ）
　　　　三角形の内角の和は１８０°であるから、∠ａ＋∠ｂ＋∠ｃ＋∠ｄ＋∠ｅ＝１８０°


……「わからなかった〜」という人でも、こう答を見せられてしまうとカンタンでしょ?
図形の中にうまいこと三角形を見出せるかどうかがポイントなんですね。