連珠 五目並べ


最終更新



ここでは、連珠 五目並べに関する情報（主にソフトに関するもの）を扱う。
河村九段との対局
コンピュータ連珠世界選手権結果
コンピュータ連珠世界選手権
posフォーマットについて
五珠二カ所打ち実装

コンピュータ連珠世界選手権優勝（参加？）への道


コンピュータ連珠選手権というものがあるらしい。
これを知ったのは ToMoさんのページ の情報を見たことによってである。（ToMoさんありがとうございます）
私は無謀にもさっそくロシアのNosovsky.A.Mさんにメールを出したのである。
何度かのやり取りで、ファイル形式などについて教えてもらい、更に、「連珠 五級の問題を解け！」と宿題を出された。もちろんコンピュータに解かせるの である。
指定のページ にいったのはいいがそこから 5級の問題のページ を見つけるのに若干の苦労（笑）をしたりしながら、なんとか問題をゲットした。
どうやらすべて「追いつめ勝ち」の問題らしい。実は私は「詰め連珠」の定義を 知らない。三や四の連続で勝ちを見つけるのか、それともミセ手もありなのか？
（そのあたりの情報をご存知の方は教えてください）

(ミセルやフクムも有りだということが分かりました、これはつらい！)
ちなみに問1-6は黒先で黒が勝ち、問7-10は白先で白が勝つ。
さっそくごもく君で盤面を作り（2人用で作る）解かせるとなんと3問しか解けなかった
これでは仕方ないのでアルゴリズムを強化することにした

連珠の思考アルゴリズムのプログラムは、どのように行うのだろうか？
私の場合は、「追い手検索」と「重み打ち」に分けて作成している。
追い手検索とは、三、三、四三、といった攻撃の連続で勝ちがあるかどうかを 検索するというものである。
重み打ちとは、ある評価関数に基づき盤面を評価してもっとも評価値の高いところ に打つというものである。
よって、まず追い手検索を行い、勝ちが見つかったらそれを打ち、見つからない 場合は重み打ちに取りかかるという形になる。
追い手検索は詰め連珠を解くのにも効果を発揮する。以下にいくつかの 「ごもく君Ver2.1」用のデータファイルを示す。
最初のファイルは、 連珠世界500号の表紙の詰め連珠（黒の四追い勝ち）である。
これを「ごもく君Ver2.1」でロードし、先手をコンピュータにすれば、あなたが どの様に守ろうがコンピュータは勝ちを見つけるはずである。
これは、初手を打つ段階で、最後の盤面まで読み切っている事を意味する。 （でないと初手が打てない）
重みで偶然という事が無いとは言えないが、思考ログを確認したので間違いない。

思考アルゴリズム強化には、他に定石データを持たせるという手法がある。
これはこの盤面ならこう打つというデータを蓄積させ（たいてい手入力？）そのとおりに打つという、アルゴリズム的にはそんなに面白く無い方法である。
まあ、回転の考慮（ある定石を入れれば回転してもそのとおり打つ）程度のアルゴリズムは必要だろうが。。。
定石を入れる際、どこまで入れるかが問題となる。まさか石が5つ並ぶまで入れていたのでは、手がつってしまう。
ここでも、追い手検索が役に立つ。追い手検索で確実に勝てるならばそこまでの定石を入れておけば良いわけである。追い手検索アルゴリズムの強化は、定石データの入力の量を軽減するわけである。

そんなこんなで、苦労の末、全ての問題が解けるアルゴリズムが完成した。
しかも、思考時間もそんなに遅くならずに（これが一番難しい）
近々公開予定である


pos形式ファイルフォーマットについて


 五珠二カ所打ち実装
　連珠正式ルールに対応するには、三手目で仮後手が黒か白を選択する、珠型交代と、 五手目に黒が石を二つ打って白がどちらかを取り除くという、五珠二カ所打ちにを実装 する必要がある。
特に、五珠二カ所打ちでは二カ所に石を打つ際、対称になってはいけない。ここで言う対称は、盤の端を考慮せずに判断する。つまり、盤が無限に続くと考えて判断するのである。
例えば、下図は盤の端を考慮すれば対称とは言えないが、考慮しなければ、対称である。よって打ってはならない。
ちなみに五手目の2カ所のポイントが5及び6である。


図1


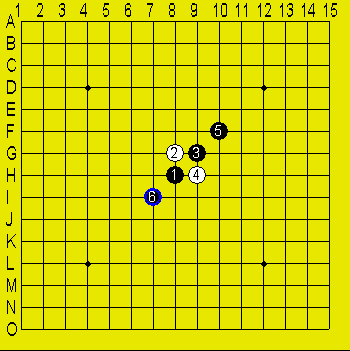
上図は点対称の例であるが、下図のように線対称な場合も打ってはならない


図2



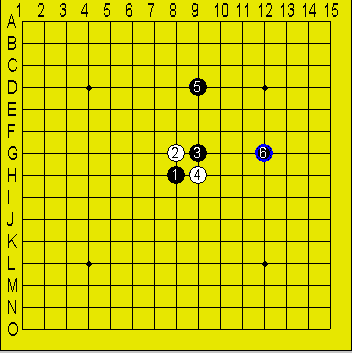
対称といっても、5手目と6手目が対称の位置に無ければ、全体が対称であっても 打っても良い。その例が下図である。
数学的には下図は対称である。しかし、5手目と6手目が対称軸に対して座標変換 した際、互いが互いの写像になっていないので問題ないのである。
これを連珠的に言えば、どちらを取り除いても（盤の端を考慮せずに）意味が同じになってしまうところに打ってはならないと言うことである。

図3



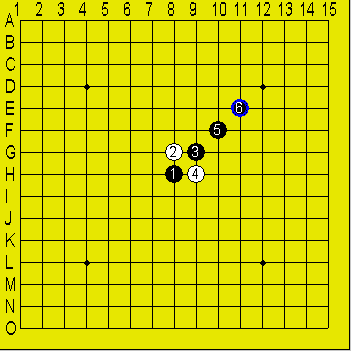
対称性の判断にはまず、盤の石のある部分だけの長方形領域を求める。
盤の端を考慮しないということは、盤が無限に続くとも考えられるが、 盤の石のある位置だけで判断すると考えることも出来るためである。
次に、長方形領域の中心を0,0として座標をつける。
5*5ならば以下の通りである。 
  -2-1 0 1 2
-2
-1　○●
 0　●○
 1　　　　●
 2　　　●

写像を求めるには座標変換を行う。変換前の座標をx, y、変換後の座標を xx,yyとすれば、 
xx =  x, yy =  y
xx = -x, yy =  y
xx =  x, yy = -y
xx = -x, yy = -y
xx =  y, yy =  x
xx = -y, yy =  x
xx =  y, yy = -x
xx = -y, yy = -x

の8通りが考えられる。
これらの変換を行い、打ってある全ての石が自分の8通りの写像のいずれかに
マッチングすれば、図形は対称であるといえる。
問題は、中心点が求められない場合である。
具体的には図1のような場合である。
それでも上記変換を行うために仮想の原点を追加する処理を行った。
x >= 0の場合x + 1、y >= 0の場合y + 1を行うと 
  -2-1 0 1 2
-2　　　●
-1　○●
 0　●○
 1●
 2

は 
  -2-1 0 1 2
-2　　　　●
-1　○　●
 0
 1　●　○
 2●
になる。
こうすれば、先ほどの座標変換が使えるというわけだ。
しかし、落とし穴もある。
例えば下図である。

図4


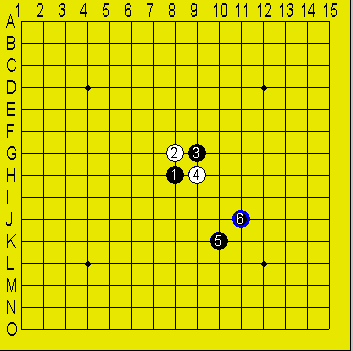
この図に仮想の原点を足場合x = 10のところに空白列を挿入した形
つまり、図5のようになる。

図5


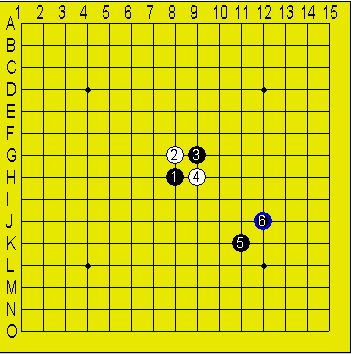
もともと対称でない図形を間違って対称と判断してしまう。
これはもともと長方形だったという情報が欠如しているためである。
よって、まず、x,yに関して、石のある範囲のx,yの値
が偶数か奇数かをそれぞれ求め、その情報を保存しておく。
偶数の場合は、仮想の原点軸を挿入する。
そして、8通りの座標変換のうち4つまでを行う。
残りの4つはxとyの入れ替えを伴うものであり、もともと石のあった領域が
長方形（正方形でない）場合、x,yの入れ替えによる対称はあり得ない。
そこで、先ほど保存した、挿入処理前の石のある範囲の値のx yが等しくない
場合は、残りの4つの変換による比較は行わない。
これで対称性の判断が出来る。
もっともこれだけでは図3も対称になってしまうので
（対称なのだが）
5手目の写像が6手目、になっているかを最後に確認する。
図6


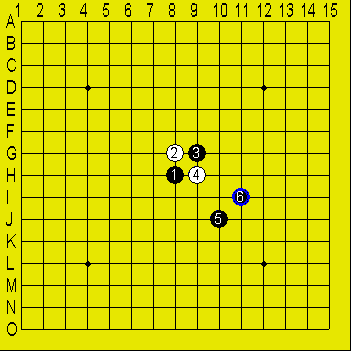
ちょっと気になるのが、図6と図5が全く同じ形に変換されたのち比較される
という点だ。これの弊害が無ければ良いと思いながら、反例を探したが、
今のところ見つかっていない。
戻る