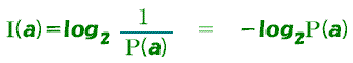|
(3)確率と情報量
情報量は、シャノン(C.E.Shannon)によって1948年にはじめて数学的に明確に示された。
自己情報量は、確率を使って次のように定義されている。
やってみよう 確率を使って、カード当てゲームの答えの自己情報量を計算してみよう。
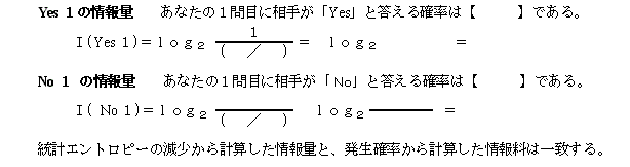
もう気づいたと思うが、対数の基本公式から、両者が等しいことはすぐに証明できる。
はじめ微視的状態がW0あり、ある事象を知ったことによってそれがW1に減ったとする。
このときの統計エントロピーの減少を計算すると
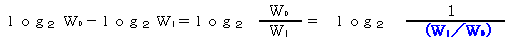 だが、 だが、
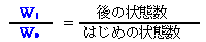 は、その事象が発生する確率Pに他ならない。 は、その事象が発生する確率Pに他ならない。
よって、以下の2つは、同じ事実の別表現であると考えて良い。
後者は、
「犬が人に噛みついてもニュースにならないが、人が犬に噛みつけばニュースになる」
といった日常の経験とよく一致する。
|