原題となる問題を解く。
問題
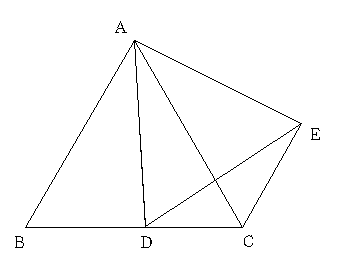
正三角形ＡＢＣをかき、辺ＢＣ上に点Ｄを取り、ＡＤを一辺とする正三角形ＡＤＥをかきます。点Ｄが、辺ＢＣ上を動くとき、点Ｅはどんな線上を動きますか。
授業の流れ
１ はじめに、問題を予想し理解する。
・Ｅの軌跡は円になるという生徒が多い。
２ 作図ツールを起動し、問題の図をかく。
・図のかきかたを説明し、図をかく。（正多角形は角数を指定するだけなので、初めてでも簡単にかける。）
３ 点Ｄを動かして、点Ｅの様子を観察し、軌跡を考える。プリントにかき、発表をする。
・直線になる。
・平行線になる。
・正三角形の辺上を動く。（点Ｅの記録を取っていくと、ほとんどの生徒が、直線上を動くことがわかる。）
４ 証明をする。
・∠ＡＣＥ＝６０゜で一定であることを証明する。
・△ＡＢＤ≡△ＡＣＥとなり、∠ＡＣＥ＝∠ＡＢＤ＝６０゜
（この証明は、生徒たちにとって経験が少ないので、合同まではすぐにできるが、その先は理解するのに時間がかかった。
条件変えによる個別の問題づくりを行う。条件変えによる、問題づくりの経験があまりなかったので、一斉授業の中で条件の変えられるところをあげてから、個別に問題を考えた。証明については、できる問題についてはやってあるが、ほとんどの問題は証明できていない。２学期以降に証明を考えてみようということになっている。
１．正三角形を正方形に変える。（これが最も多かった。）
２．正五角形（正六角形）に変える。各点の軌跡を表す直線が１点で交わる。
生徒はこの問題くらいしか作ってなかったのですが、これは、たくさん問題ができます。点Ｆをとなりの辺のBC上にとることもできますし、ＤＥ上、この図のようにＣＤ上にとることもできます。この場合、ＡＥとＣＤの延長上の交点Ｐで交わる。証明2
３．二等辺三角形に変える。
点Ｅの軌跡は同じように直線になります。この場合、頂角を等しくかいたので２つの二等辺三角形は相似になり、頂点Ｃを通ります。
４．２種類の図形を組み合わせる。（はじめの図形を正方形、正方形の辺上に点を取りそこに正三角形を作るなど。）
５．ＡＢＣＤが正方形。ＢＥＦは直角二等辺三角形。点Ｆが、Ａ、Ｄ、Ｏ、Ａと動くとき点Ｅの軌跡はどうなるか。
点が直線上を動くのでなく、決まった図形上を動くときどうなるかを考えた問題です。はじめの問題からはずいぶん変わっているようにも見えますが、直角二等辺三角形も正方形を半分にしたものですから、ＤＯ、ＯＡ上を動くところが大きく変わっているところでしょう。
６．正三角形の重心をとって、その点と辺上の点を使って正三角形をかく。もう一つの頂点が正三角形になる。
頂点Ａを変えた問題です。特に点を指定する必要もなかったようなのですが、特別な点ということで重心を選んだようです。（ＧＭのメニューに重心はありますから簡単にとれます。）これも、図形を変えたり、点の位置を重心以外にすれば、いろいろな問題が考えられそうです。
１番の点Ｇについての証明と５番については、問題を作った生徒たちが１学期のうちに証明を済ませました。合同を使えば、はじめの時間にやった問題と同じようにできるので結構簡単にできます。それ以外の証明ですが、簡単にできそうもないので、２学期以降少しずつみんなでやっていこうかとなっています。
作図ツールの部屋に戻る